Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas Revisão - Ex. 184

A força transversal P   é aplicada, como mostrado, na extremidade A   de um tronco de cone A B .   Denotando por d 0 o diâmetro em A ,   mostre que a máxima tensão normal ocorre no ponto H ,   que está contido em uma seção transversal de diâmetro d = 3 2 d 0 .

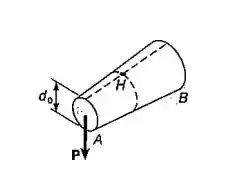
Passo 1

Fala aí galera do Responde aí, bora amassar na prova de resmat. Primeiramente, sabemos que:

σ = M W

Onde W = I y .   A equação do momento será:

M = - P x

Logo:

W = π r 4 4 d 2 → W = π d 3 32

Para achar d , usaremos a equação da reta:

y = a x + b

d = k x + d 0

Logo:

W = π k x + d 0 3 32

σ = M W →   σ = - P x π k x + d 0 3 32 = - 32 P x π k x + d 0 3

Devemos derivar e igualar a 0   para encontrar o máximo da função. Logo:

σ ' = 1 k x + d 0 3 - 3 x k x + d 0 2 k k x + d 0 6

Isolando k x :

k x = d 0 2

Logo:

d = k x + d 0 = d 0 2 + d 0 = 3 d 0 2

Portanto, está provado!

Resposta

d = 3 d 0 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, domensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 825k P a .
Para a viga com o carregamento mostrado, dimensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 860k P a .
Para a viga com o carregamento mostrado, domensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 825k P a .
Para a viga com o carregamento mostrado, domensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 825k P a .
Para a viga com o carregamento mostrado, domensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 825k P a .