Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas Revisão - Ex. 178
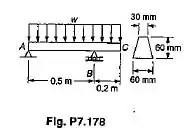
Uma barra maciça de aço tem uma seção transversal trapezoidal e suporta uma carga uniformemente distribuída como mostrado. Sabendo-se que na tração e na compressão, determine a carga admissível que pode ser suportada.
Passo 1
Fala aí galera, bora pra mais essa questão de resmat. Para determinar a máxima carga distribuída, temos que calcular as tensões de tração e compressão em função de e escolher o menor valor encontrado para a carga.
Sabemos que o maior momento atua no apoio B, portanto, lá está a maior tensão. Pegando este ponto:
A fórmula da tensão normal é:
Onde é o momento na seção, é a distância da linha neutra e é o momento de inércia da seção.
Passo 2
Para determinar a tensão, devemos encontrar o momento de inércia da seção e a posição do centroide, que coincide com a posição da linha neutra. O centroide de um trapézio é dado por:
Agora, vamos calcular o momento de inércia:
Agora, basta calcular as tensões e igualar às tensões admissíveis:
Passo 3
Agora, vamos escolher o valor máximo de que será admitido pela estrutura. Se simplesmente pegarmos o maior (compressão)estaremos subdimensionando a carga, pois a força ultrapassará a tensão máxima de tração. Logo, devemos escolher o menor valor para