Em uma investigação do “efeito de chicote” resultante de colisões trasieras, a rotação brusca da cabeça é modelada utilizando uma esfera maciça homogênea de massa e raio que gira em torno de um eixo tangente (no pescoço) para representar a cabeça. Se o eixo em recebe uma aceleração constante com a cabeça inicialmente em repouso, determine expressões para a aceleração angular inicial da cabeça e sua velocidade angular em função do ângulo de rotação. Assuma que o pescoço está relaxado de modo que nenhum momento é aplicado à cabeça em .

Passo 1
Vamos começar procurando uma expressão para a aceleração angular inicial. Para isso vamos descobrir como ela se relaciona com a aceleração do centro de massa :
Essa equação te diz que a aceleração do centro de massa é a aceleração do ponto (que foi dada pelo ennciado) somada vetorialmente à aceleração de em relação ao ponto .
Assim que ocorre a colisão traseira, a cabeça será “jogada para trás” com aceleração angular em torno do ponto onde ela está presa ao pescoço:
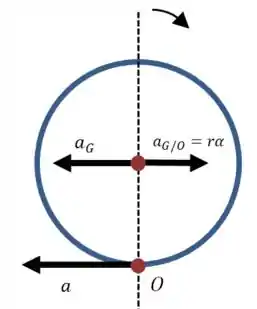
Então podemos escrever nossa equação da seguinte forma:
Tirando o módulo dos dois lados:
Essa é nossa primeira equação, precisamos achar algum jeito de substituir , para que possamos encontrar .
Passo 2
O enunciado também disse que o pescoço está relaxado de modo que nenhum momento é aplicado à cabeça em , ou seja:
E agora vamos igualar isso à expressão para a soma de momentos em torno de um ponto qualquer em um corpo rígido (que nesse caso é a cabeça):
O momento de inércia da esfera em relação a um eixo que passa por é:
E nesse caso a distância entre e (centro de massa) é o raio da esfera e :
E o sinal negativo apareceu porque (conforme o nosso desenho), o momento associado a favorece a rotação no sentido oposto a .
Podemos substituir isso na equação de cima para encontrar :
Passo 3
Agora queremos encontrar uma expressão para a velcidade angular em função do ângulo . Em geral, quando queremos encontrar , precisamos usar a seguinte equação:
Ou seja, precisamos encontrar uma função que sejá válida para qualquer instante, não apenas o inicial.
Então vamos escrever outra equação de momentos em relação ao ponto . Nesse caso, todas as forças no contato do pescoço terão momento nulo, e ficaremos apenas com o momento da força peso:
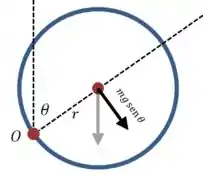
Agora vamos montar o resto da equaçao:
E o sinal negativo aparece pelo mesmo motivo de antes. Além disso, podemos usar a expressão que já conhecemos para :
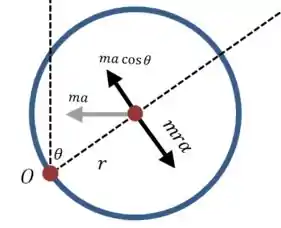
Agora vamos dividir tudo por e isolar :
Passo 4
E agora vamos substituir essa função na equação de cima:
E agora vamos integrar, fazendo ir de até , e ir de até um qualquer:
E resolvendo cada um dos termos dessa integral, vamos achar o seguinte:
Então:
Resposta
A aceleração angular inicial é , e a velocidade angular é .