Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 27

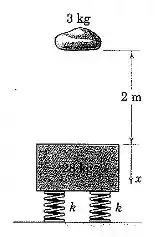
27. Um pedaço de 3   k g de massa de vidraceiro cai de uma altura de 2   m sobre o bloco de 28   k g inicialmente parado, que é apoiado por quatro molas, cada uma das quais possui uma constante k = 800   N / m . Determine o deslocamento x como uma função do tempo durante a vibração resultante, onde x é medido a partir da posição inicial do bloco, como mostrado.

Passo 1

Bom, primeiro a gente vai calcular a massa de 3   k g depois de cair 2   m , sabendo que ela caiu dessa altura, ou seja, a velocidade inicial é zero:

v 2 = v 0 2 + 2 g h

Onde h é a altura e g a acelreação da gravidade

v = 2 g h

v = 2 ( 9,81   m / s 2 ) ( 2   m )

v = 2 ( 9,81   m / s 2 ) ( 2   m )

v = ( 39,24   m 2 / s 2 )

∴ v = 6,26   m / s

Passo 2

Agora, a gente vai calcular a deformação estática adicional δ na mola devido à massa de 3   k g .

Bom, primeiro faremos o somatório de forças no eixo y

∑ F y = 0

m g - k δ = 0

m g = k δ

δ = m g k

Mas, devemos multiplicar a constante k por 4 , pois são 4 molas presentes

δ = ( 3   k g ) ( 9,81   m / s 2 ) 4 ( 800   N / m )

δ = 9,20 × 10 - 3   m

Passo 3

Aqui, vamos calcular a velocidade x ˙ 0   ( v 0 ) após o impacto. Pela conservação da quantidade de movimento, temos que:

m + M ⋅ x ˙ 0 = m v

Onde m é a massa de 3   k g , M é a massa do bloco de 28   k g

3   k g + 28   k g ⋅ x ˙ 0 = ( 3   k g ) ( 6,26 m / s )

x ˙ 0 = ( 3   k g ) ( 6,26 m / s ) 3   k g + 28   k g

x ˙ 0 = 0,606   m / s

Passo 4

Enfim, calcularemos a frequência natural de oscilação da mola ω n pela fórmula:

ω n = k m

Lembrando que devemos multiplicar k por 4

ω n = 4 ( 800 N / m ) ( 31   k g )

ω n = 103,23

∴ ω n = 10,16   r a d / s

Passo 5

Com todas essas informações, podemos montar a equação de deslocamento x como função do tempo da seguinte maneira:

x = δ + x 0 ⋅ cos ⁡ ω n t + x ˙ 0 ω n ⋅ s e n ( ω n t )

x = 9,20 × 10 - 3   m + 9,20 × 10 - 3   m ⋅ cos ⁡ 10,16 t + 0,606   m / s 10,16   r a d / s ⋅ s e n ( 10,16 t )

∴ x = 9,20 × 10 - 3 1 - cos ⁡ 10,16 t + 59,7 × 10 - 3 ⋅ s e n 10,16 t   ( m )

Resposta

A equação que descreve o deslocamento x como uma função do tempo é:

x = 9,20 × 10 - 3 1 - cos ⁡ 10,16 t + 59,7 × 10 - 3 ⋅ s e n 10,16 t   ( m )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a razão entre as amplitudes de duas oscilações sucessivas é constante para um oscilador linearmente amortecido.
Um oscilador linearmente amortecido possui um fator Q igual a 20 . (a) Qual é a fração de redução da energia, em cada ciclo? (b) Use a equação para determinar a diferença percentual entre ω ' e ω 0 .
Um oscilador tem um período de 3,00s . Sua amplitude diminui 5,00 por cento em cada ciclo. (a) De quanto diminui sua energia mecânica em cada ciclo? (b) Qual é a constante de tempo τ ? (c) Qual é o fa
Um corpo de 2,00k g oscila preso a uma mola, com uma amplitude inicial de 3,00c m . A constante de força da mola é 400N / m . Determine (a) o período e (b) a energia total inicial. (c) Se a energia di
Um sistema massa-mola linearmente amortecido oscila a 200H z . A constante de tempo do sistema é 2,0s . Em t = 0 , a amplitude de oscilação é 6,0c m e a energia do sistema oscilante é 60J . (a) Quais