Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 223
2/223)Sob aação da força P , aaceleração constante do bloco B é de para cima do plano inclinado . Para o instante em que a velocidade de é de subindo o plano inclinado , determine a velocidade de em relação a , a aceleração de em relação a e a velocidade do ponto do cabo .
Passo 1
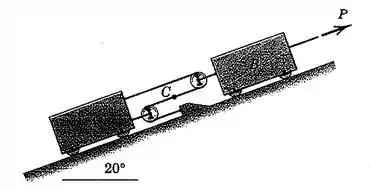
Então galera, para resolvermos exercícios desse tipo , devemos primeiramente calcular o comprimento do cabo que aparece na imagem . E para isso , definimos que :
é a distância do centro da polia mais à esquerda até um anteparo mais à esquerda do sistema mostrado no enunciado .
é a distância do centro da polia mais a direita até o anteparo citado no item anterior .
é a distância entre o ponto e o mesmo anteparo citado anteriormente .
Com isso definido , achamos que o comprimento do cabo é dado por :
Passo 2
Agora derivamos a equação do compimento do cabo para acharmos uma relação com as velocidades :
Com raciocínio análogo ao procedmento anterior , derivaremos a equação das velocidades para obtermos uma relação com as acelerações :
Então , substituindo os valores fornecidos pelo enunciado :
Passo 3
Bom galera ,a velocidade de em relação a é dada pela subtração :
Usando um raciocínio análogo ao item anterior , a aceleração de em relação a , por sua vez , é dada pela relação :
Passo 4
Então pessoal , usando as propriedades que definimos no passo 1 , o comprimento do cabo entre e é dado por :
Derivando para obtermos a relação entre as velocidades :
Sendo assim , achamos que :
Resposta
E aí , topa fazer mais exercícios com a gente?