Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas fundamentais - Ex. 9
Localize o centroide da área da seção transversal da viga.
Passo 1
Vamos considerar o eixo passando pelo ponto que divide a viga em duas partes iguais:
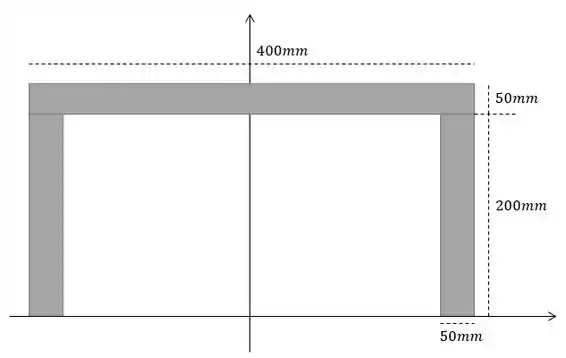
Como a figura é simétrica, a gente já sabe que o centro de massa está só sobre o eixo , sem componente em ! A figura está então dividida em duas barras verticais e uma horizontal. Para as verticais, o do centro de massa é . Para a horizontal, o do centro de massa .
Passo 2
A gente já pode partir direto pra fórmula do centroide!
Resposta
Exercícios de Livros Relacionados
Localize o centro de massa ( x - ,y - ,z - ) do sólido homogêneo.
Localize o centro de massa z - do sólido formado escavando-se um hemisfério na base do cilindro com um cone no topo. O cone e o cilindro são feitos de materiais com densidades de 7,80M g / m 3 e 2,70M
Um foguete de brinquedo consiste em um topo cônico sólido, ρ t = 600k g / m 3 , um cilindro oco, ρ c = 400k g / m 3 e uma vara com uma seção transversal circular, ρ v = 300k g / m 3 . Determine o comp
Localize o centro de massa z - do sólido consistindo em um núcleo central cilíndrico A , com densidade de 7,90M g / m 3 , uma parte externa cilíndrica B e um cone C no topo, cada um desses dois último
Um furo com raio r deve ser feito no centro do bloco homogêneo. Determine a profundidade h do furo de modo que o centro de gravidade G seja o mais baixo possível.