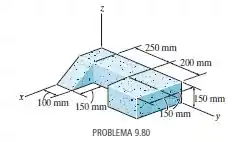
Localize o centro de massa do sólido homogêneo.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Nesse problema foi dado um objeto com várias partes e nosso objetivo é encontrar o centro de massa .
Parece complicado?
Para resolver esse problema podemos separar esse objeto em partes mais simples e substituir na fórmula
Lembrando que no enunciado foi dito que o objeto é homogêneo, então seu centro de massa é o mesmo que seu centroide.
Bora começar!
Passo 2
Podemos dividir esse objeto em três partes:
- O paralelepípedo de dimensão
- A rampa de dimensão
- E outro paralelepípedo de dimensão
- Para :
- Para :
- E por fim, para :
Dessa forma, temos:
É isso! Entendeu tudo? Responde Aí!