Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 22
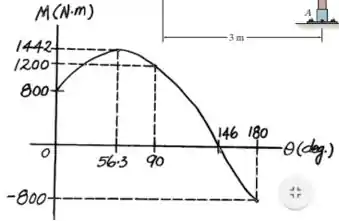
Determine o momento da força em relação ao ponto como uma função de . Represente os resultados de (ordenada) em função de (abscissa) para .
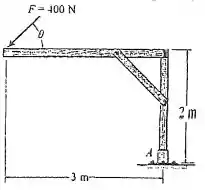
Passo 1
O momento gerado pela força poderá ser determinado através de suas componentes aplicando o princípio dos momentos, fazendo a soma dos produtos entre essas componentes e as distâncias do braço de momento.
Passo 2
Dessa forma, considerando que o momento positivo atue no sentido horário, tem-se que:
Passo 3
Um ponto que pode ser definido para ser plotado no gráfico é o ângulo para obter o momento máximo. O momento máximo ocorrerá quando:
Rearranjando esta equação:
Assim,
Graficamente:
Resposta
Exercícios de Livros Relacionados
Dados os três vetores não nulos A , B e C , mostre que se A ∙ B × C = 0 , os três vetores necessitam estar no mesmo plano.
Se o momento produzido pela força de 4k N em relação ao ponto A é 10k N . m no sentido horário, determine o ângulo θ , onde 0 ° ≤ θ ≤ 90 ° .
Se A , B e D são vetores, prove a propriedade distributiva para o produto vetorial, ou seja, A × B + D = A × B + ( A × D ) .
Prove a identidade do produto triplo escalar A ∙ B × C = A × B ∙ C .
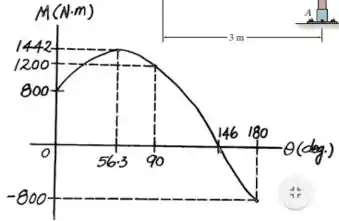
Se θ = 45 ° , determine o momento produzido pela força de 4k N em relação ao ponto A .