Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 54

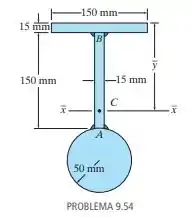
Determine a localização y do eixo x–x que passa pelo centroide da área transversal da viga. Para o cálculo, desconsidere o tamanho das soldas nos cantos em A e B.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Vamos começar com a área da parte retangular

A 1 = 150 × 15

A 1 = 2250   m m 2

A área da parte retangular

A 2 = 150 × 15

A 2 = 2250   m m 2

A área da parte circular

A 3 = π × 50 2

A 3 = 7854   m m 2

Passo 2

Coordenadas do centroide de cada parte

y 1 = 15 2

y 1 = 7.5   m m

y 2 = 15 + 150 2

y 2 = 90   m m

y 3 = 15 + 150 + 50

y 3 = 215   m m

Passo 3

Agora iremos calcular o centroide ára o eixo de y

y c = A 1 y 1 + A 2 y 2 + A 3 y 3 A 1 + A 2 + A 3

y c = 2250 × 7.5 + 90 × 2250 + 7854 × 215 2250 + 2250 + 7854

y c = 16875 + 202500 + 1688610 12354

y c = 154.44   m m

Passo 4

Logo, por simetria:

x - = 150 2 = 75   m m

Resposta

x - = 75   m m

y - = 154.44   m m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide da área da seção transversal da viga construída.
Localize o centroide da área da seção transversal da viga de concreto.
A treliça é composta de sete membros, cada um tendo uma massa por unidade de comprimento de 6 k g / m . Localize a posição do centro de massa. Despreze a massa das placas de ligação nas juntas.
Localize o centroide do fio uniforme dobrado na forma mostrada.
Localize a distância y - até o centroide da área da seção transversal do membro.