Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas fundamentais - Ex. 7
Localize o centroide do fio dobrado na forma mostrada.
Passo 1
Falaa galerinha, tudo beleza? Nesse exercício aqui, o enunciado nos deu um fio dobrado como na figura a seguir:
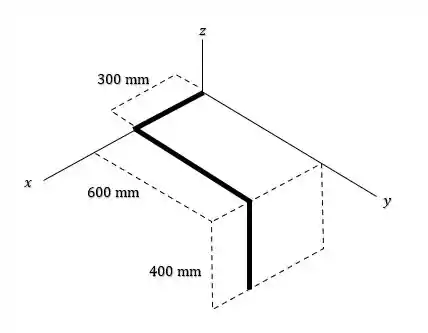
Sabendo das dimensões que a figura mostra, o enunciado quer que a gente encontre o centroide do fio dobrado.
Iradoso, pra isso podemos dividir o fio em partes tal que:
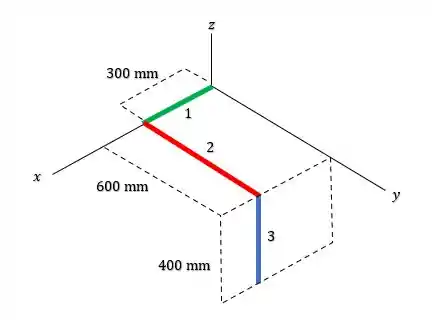
Sendo assim podemos aplicar as equações para figuras compostas para encontrar o centroide do fio, dada como:
Passo 2
Belezoca, agora que a já dividimos o fio dobrado em , podemos montar uma tabelinha com as posições do centroide de cada parte, tal que:
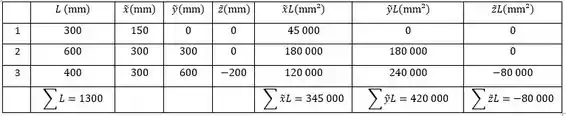
Sendo assim, obtemos as coordenadas do centroide do fio, de modo que no eixo :
Agora no eixo :
E por fim para o eixo :
Resposta
Exercícios de Livros Relacionados
Determine a distância x - até o centroide do sólido que consiste em um cilindro com um furo de profundidade h=50m m escavado em sua base.
Determine a profundidade h do furo no cilindro de modo que o centro de massa do sólido estejalocalizado em x - = 64m m . O material tem densidade de 8M g / m 3 .
Determine a localização x - do centroide C da área sombreada que faz parte de um círculo com raio r .
Determine a localização x - do centroide C da área sombreada que faz parte de um círculo com raio r .
Localize o centro de massa z - do sólido. O material tem densidade ρ = 3M g / m 3 . Há um furo com diâmetro de 30m m conforme a figura.