Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 94
O cabo suporta a lâmpada de e a lâmpada de . Determine a tração máxima no cabo e a flecha do ponto .
Passo 1
O problema quer que a gente encontre a flecha e a tração máxima no cabo.
Vamos começar calculando o momento, tendo como eixo de rotação:
Agora vamos calcular o somatório das forças do sistema em equilíbrio:
No eixo :
Passo 2
Vamos analisar a junta :
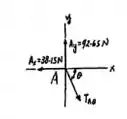
No eixo fica:
Calculando o sistema de equações:
Assim, obetermos:
Com isso, também já obtemos :
Passo 3
E por fim, fazemos o mesmo na junta :
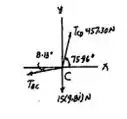
E assim também temos:
Resposta
Exercícios de Livros Relacionados
Determine a força em cada membro da treliça carregada.
Determine a força no membro C G da treliça carregada. Suponha que as quatro reações externas em A , B , E e F são iguais em magnitude e são direcionadas perpendicularmente à superfície de suporte loca
Encontre as forças nos membros EF, KL e GL para a treliça Fink mostrada.
Uma pequena roda-gigante é construída com duas treliças idênticas, uma das quais é mostrada. O membro AO é temporariamente removido para substituição. Se o peso das cadeiras e membros estruturais resu
Determine os diagramas de esforço cortante e de momento fletor para a viga.