Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas - Ex. 118
A estrutura de quatro membros na gome de um é sustentada em e por colares lisos e, em , por um pino. Todos os outros nós são juntas esféricas. Se o pino em falhará quando a porça resultante nele for , detemrine a maior força vertical que pode ser suportada pela estrutura. Além disso, quais são as componentes de força que o membro exerce sobre os membros e ? Os colares em e e o pino em só exercem componentes de força sobre a estrutura.
Passo 1
Vamos separar o diagrama de corpor livre em três partes, beleza? A primeira será a estrutura maior.
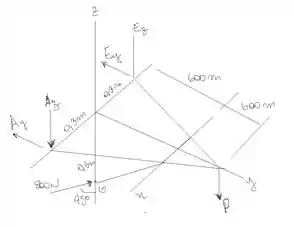
Para um corpo em equilíbrio, tanto o somatório dos momentos quanto o somatório das forças é igual a zero. Assim, calculando o momento em relação aos eixos e adotando como sentido positivo o anti-horário para o momento e para cima e para direira para as forças, temos:
Passo 2
Vamos olhar para a segunda parte do diagrama de corpo.
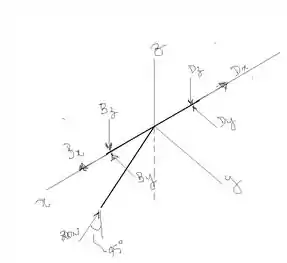
Para um corpo em equilíbrio, tanto o somatório dos momentos quanto o somatório das forças é igual a zero. Assim, calculando o momento em relação aos eixos e adotando como sentido positivo o anti-horário para o momento e para cima e para direira para as forças, temos:
Passo 3
Por último, vamos olhar a terceira parte do diagrama de corpo livre.
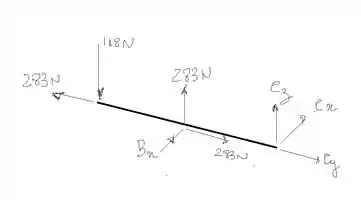
Para um corpo em equilíbrio, o somatório dos momentos é igual a zero. Assim, calculando o momento em relação aos eixos e adotando como sentido positivo o anti-horário, temos:
Resposta
As forças são: