Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 94
A longarina ABD da asa de um avião leve é feita de alumínio 2014-T6 e tem área de seção transversal de , profundidade de e momento de inércia em torno de seu eixo neutro de . Determine a tensão de flexão máxima absoluta na longarina se a carga for a mostrada na figura. Considere que , e são pinos. O acoplamento é feito ao longo do eixo longitudinal central da longarina.
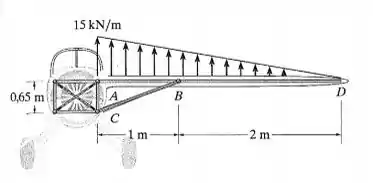
Passo 1
Primeiro, vamos fazer o DCL e determinar as reações:
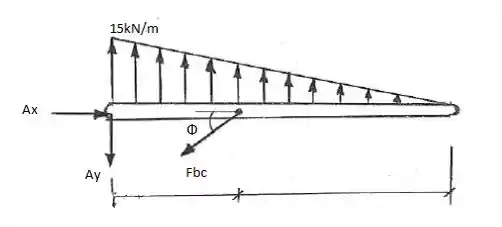
Temos que:
Fazendo o diagrama de momento, temos:
O momento máximo vale 6,667kNm.
Passo 2
Calculando-se a tensão, temos:
Resposta
Exercícios de Livros Relacionados
Cinco tiras de metal, cada uma com 40 mm de largura, são firmemente unidas, de maneira a formar a viga composta mostrada. Os módulos de elasticidade são de 210G P a para o aço, 150G P a para o latão e
Um tubo de aço e um de alumínio são firmemente unidos para formar a viga composta mostrada. Os módulos de elasticidade valem 200G P a para o aço e 70G P a para o alumínio. Para um momento fletor de 1,
Um tubo de aço e um de alumínio são firmemente unidos para formar a viga composta mostrada. Os módulos de elasticidade valem 200G P a para o aço e 70G P a para o alumínio. Para um momento fletor de 1,
Um tubo de aço e um de alumínio são firmemente unidos para formar a viga composta mostrada. Os módulos de elasticidade valem 200G P a para o aço e 70G P a para o alumínio. Para um momento fletor de 1,
Um momento de 7,5k N m é aplicado ao perfil de aço laminado S 310 x 74 mostrado. Pede-se:Sendo que o momento encurva a viga em torno de um eixo horizontal, determinar a máxima tensão e o raio de curva