Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 93
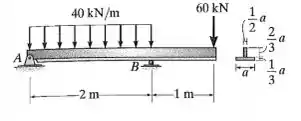
A viga está sujeita ao carregamento mostrado na figura. Determine a dimensão a exigida para sua seção transversal se a tensão admissível para o material for σmáx = 150 MPa.
Passo 1
Falaa galerinha bonita, tudo belezinha com vocês?!
Saca só, nesse exercício aqui o enunciado nos diz que a viga está sujeita ao carregamento mostrado na figura. Sabendo que a tensão admissível para o material é:
O enunciado pede pra gente determinar a dimensão exigida para a seção transversal da viga!!
Belezoca, pra gente achar esse valor, precisamos achar a expressão para a tensão máxima do momento em função de e comparar com essa tensão dada.
Vamos usar essa fórmulinha:
Bora lá!
Passo 2
Nessa fórmula, é o momento de inércia da nossa seção em relação ao eixo . Para achar ele, precisamos primeiro achar o centroide da seção. Vamos dividir ela assim:
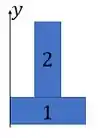
O centroide fica:
Aí para achar o momento de inércia vamos usar o teorema dos eixos paralelos:
Então como é a maior distância entre e a borda da seção, obtemos que:
Passo 3
Falta , que é o momento máximo na viga.
Precisamos então ver onde o momento nessa viga é máximo. Podemos ver isso pelo diagrama de momento fletor.
Primeiro a gente acha as reações de apoio pelas equações de equilíbrio. Considerando que elas estão para cima.
Logo:
Do mesmo modo, vamos ter que:
Sendo assim:
Com isso, achamos as equações de momento para as seções e :
Seção 1, :
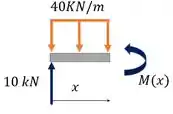
Seção 2,
Aí a gente faz o diagrama:
Como podemos ver, o momento máximo vale 60kNm.
(usamos a conveção do diagrama de que para cima temos o momento negativo)
Passo 4
Agora vamos montar nossa tensão máxima e comparar com a tensão dada
Isolando