Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 91

Uma matriz de aço, mostrada em seção, tem a forma de um sólido gerado pela rotação da área sombreada em torno do eixo z. Calcule a massa m da matriz.

Passo 1

Nesta tarefa, precisamos determinar a massa do elemento.

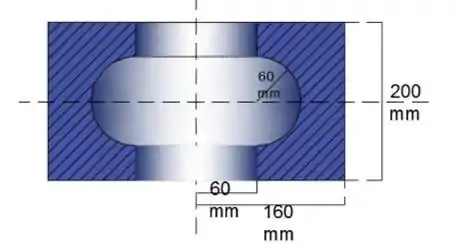
Primeiro, vamos determinar p centroide retangular da parte 1

r 1 ¯ = 60 + b 2 = 60 + 100 2 = 110 m m

Calcularemos a área retangular da parte 1

A 1 = b ⋅ L = 100 + 200 = 20000 m m 2

Passo 2

Determinaremos o centroide retangular da parte 2

r 2 ¯ = 60 + 4 r 3 π = 60 + 4 ⋅ 60 3 π = 85.465 m m

Calcularemos a área retangular da parte 2

A 2 = π r 2 2 = π 60 2 2 = 5654.867 m m 2

Passo 3

Determine o volume da secção

V = 2 π F A = 2 π r 1 ¯ A 1 - r 2 ¯ A 2 = 2 π ( 110 ⋅ 20000 - 56.465 ⋅ 5654.867 ) = 2 π ⋅ 1716706.792 = 10790000 m m 2

Por fim, vamos determinar a massa do elemento

m = ρ V = 7830 ⋅ 10790000 m m 3 ⋅ 10 - 9 m 3 1 m m 3 = 84.5 k g

Resposta

m = 84.5 k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centro de massa z - do sólido. O material tem densidade ρ = 3M g / m 3 . Há um furo com diâmetro de 30m m conforme a figura.
Localize o centro de massa ( x - ,y - ,z - ) do sólido homogêneo.
Localize o centro de massa z - do sólido formado escavando-se um hemisfério na base do cilindro com um cone no topo. O cone e o cilindro são feitos de materiais com densidades de 7,80M g / m 3 e 2,70M
Um foguete de brinquedo consiste em um topo cônico sólido, ρ t = 600k g / m 3 , um cilindro oco, ρ c = 400k g / m 3 e uma vara com uma seção transversal circular, ρ v = 300k g / m 3 . Determine o comp
Localize o centro de massa z - do sólido consistindo em um núcleo central cilíndrico A , com densidade de 7,90M g / m 3 , uma parte externa cilíndrica B e um cone C no topo, cada um desses dois último