Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 41
Determine o valor máximo do ângulo θ para o qual a barra fina e uniforme permanecerá em equilíbrio. O coeficiente de atrito estático em A é μA = 0,80, e o atrito associado ao pequeno rolo em B pode ser desprezado.
Passo 1
O enunciado pede que a gente determine o valor máximo do ângulo θ para o qual a barra fina e uniforme permanecerá em equilíbrio
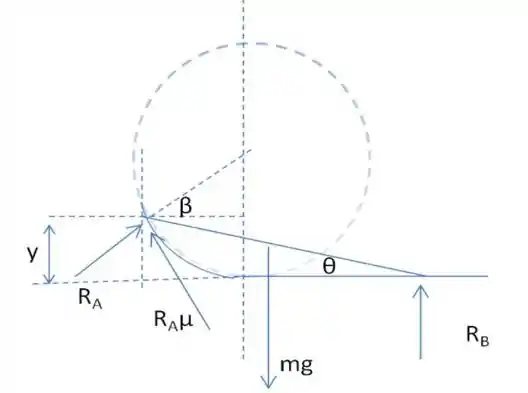
Passo 2
Na figura acima, a distância y é
E
Para equilíbrio na direção horizontal
Agora usando como referência o triângulo de lados
Resposta
Exercícios de Livros Relacionados
As caixas A e B pesam 1000N e 750N , respectivamente. Elas estão conectados por um cabo e colocadas no plano inclinado. Se o ângulo θ for aumentado gradualmente, determine θ quando as caixas começarem
Se o centro de gravidade das mesas empilhadas está em G e a pilha pesa 500N ( ≈ 50k g ), determine a menor força P que o menino precisa empurrar na pilha a fim de causar um movimento. O coeficiente de
O depósito de papel toalha contém dois rolos de papel. O que está em uso é chamado de rolo principal A e o outro é o rolo de apoio B . Eles pesam 10N e 25N , respectivamente. Se os coeficientes de atr
O refrigerador tem um peso de 900N ( ≈ 90k g ) e respousa sobre um piso cerâmico para qual μ s = 0,25 . Além disso o homem tem peso de 750N ( ≈ 75k g ) e o coeficiente de atrito estático entre o piso
Dois blocos A e B têm peso de 50N e 30N , respectivamente. Eles estão apoiados no planos inclinado para qual os coeficientes de atrito estático são μ A = 0,15 e μ B = 0,25 . Determine o ângulo que cau