Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 20
Um momento de é aplicado à barra de aço mostrada. Pede-de:
- Sendo que o momento encurva a barra em torno do eixo horizontal, determinar a máxima tensão e o raio de curvatura;
- Resolver a parte a), considerando que a barra é encurvada em torno do eixo vertical pelo momento de . Usar
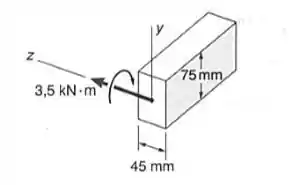
Passo 1
Nossos objetivos são dois, determinar a máxima tensão e o raio de curvatura, sabemos que a fórmula da tensão é dada por:
E o raio da curvatura é calculado da seguinte maneira:
Como queremos o raio de curvatura, podemos definir como:
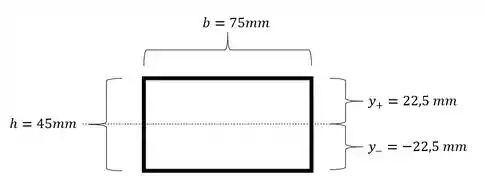
Pelo enunciado temos os seguintes dados comuns ao item A) e B).
E por ser um retângulo, sabemos que a LN ocorre no meio termo da seção, o que já facilita a nossa vida.
E precisamos do momento de inércia e dos valores de Y, porém isso varia de acordo com a orientação da encurvatura da nossa seção, então para isso iremos dividir o cálculo.
Passo 2
Vamos definir primeiro o momento de inércia e y teremos que:
- Para o item A) a encurvatura ocorre em torno da horizontal, sendo assim teremos que a nossa seção será dada por:
- Para o item B) a encurvatura ocorre em torno da vertical, e pode parecer que a conta será o mais difícil, mas o que podemos fazer é girar a seção, e ai o nosso eixo vertical se torna horizontal, e toda a conta volta a ser o que já sabemos , sendo assim teremos que a nossa seção será dada por:
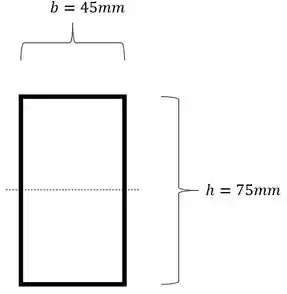
E sabemos que o momento de inercia será calculado por:
E para determinação do y teremos que:
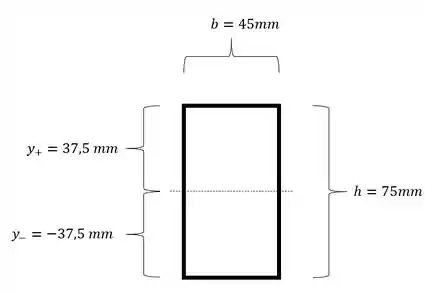
Determinando as nossas tensões, teremos que:
E determinando a curvatura, teremos que:
Passo 3
Vamos definir primeiro o momento de inércia e y teremos que:
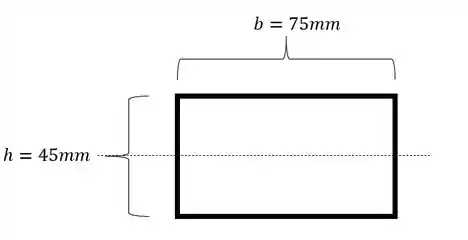
E sabemos que o momento de inercia será calculado por:
E para determinação do y teremos que:
Determinando as nossas tensões, teremos que:
E determinando a curvatura, teremos que:
Resposta
- e
- e