Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 146

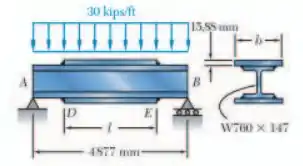
Duas placas de reforço, cada uma com 15,88   m m de espessura, são soldadas a uma viga W 760 × 147 . Conforme mostra a figura. Sabendo que l = 2743   m m e b = 304,8   m m , determine a tensão normal máxima em uma seção transversal ( a ) no centro da viga e ( b ) imediatamente à esquerda de D .

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora estudar mecânica e garantir aquele notão na prova.

Primeiro, vamos encontrar as reações aplicando as equações de equilíbrio. Como nossa viga é simétrica, podemos dizer que F A = F B . Logo:

∑ F y = 0 30 16 - 2 F A = 0 F A = F B = 240   k i p s

Em seguida, vamos calcular a equação de momento fletor a partir do ponto A , temos:

∑ M = 0 - 240 x + 30 x x 2 - M = 0 M = - 240 x + 15 x 2

Com isso, podemos encontrar os momentos em C e D . São eles:

M C = 11520   k i p ∙ i n M D = 7875   k i p ∙ i n

Assim, o momento máximo vai ser no ponto C .

Passo 2

Agora que já temos o momento máximo absoluto, basta encontrar as outras variáveis das quais a tensão depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:

σ = M c I

Onde c   é a distância da linha neutra (onde a tensão é nula) até o ponto em que queremos saber a tensão e I   é o momento de inércia da seção.

Como queremos a máxima tensão, pegaremos o maior c .   Portanto,:

c = 29,7 2 c = 15,475   i n

E para o momento de inércia, temos:

I = I t r a v e + 2 I p l a c a I = 3990 + 2 12 0,625 29,7 2 + 0,625 2 2 + 1 12 12 0,625 3 I = 7439   i n 4

Passo 3

Agora, temos todos os dados para obter a tensão normal .   Substituindo os valores, vamos encontrar a tensão normal no centro da viga:

σ = M c I

σ = 11520 15,475 7439 σ = 24   k s i

Em seguda, para obtermos a atenção no ponto D vamos usar a seguinte relação: σ = M S

Onde S = 269   i n 3 . Substituindo:

σ = M S σ = 7875 269 σ = 29,3   k s i

Resposta

σ = 24   k s i

σ = 29,3   k s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga está sujeita ao carregamento mostrado na figura. Se a dimensão de sua seção transversal a = 180 mm, determine a tensão de flexão máxima absoluta na viga.
O barco pesa 11,5k N e tem centro de gravidade em G . Se estiver apoiado no reboque no contato liso A e preso por um pino em B , determine a tensão de flexão máxima absoluta desenvolvida na escora pri
A longarina ABD da asa de um avião leve é feita de alumínio 2014-T6 e tem área de seção transversal de 1.000 m m ² ², profundidade de 80m m e momento de inércia em torno de seu eixo neutro de 1,662 10
A peça de máquina feita de alumínio está sujeita a um momento M = 75 N.m. Determine a tensão de flexão criada nos pontos B e C da seção transversal. Trace um rascunho dos resultados sobre um elemento
A viga está sujeita a um momento M. Determine a porcentagem desse momento à qual resistem as tensões que agem nas pranchas superior e inferior A e B da viga.