Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 142a
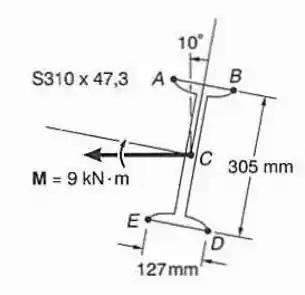
O momento atua em um plano vertical e está aplicado a uma viga orientada como mostrado. Determinar: (a) o ângulo que o eixo neutro forma com o plano horizontal.
Passo 1
Para calcular o ângulo entre a linha neutra e o plano () vamos ter de utilizar a seguinte equação:
Onde, e o ângulo é igual à soma de com .
Passo 2
Então vamos seguir nosso passo-a-passo e calcular o momento de inércia desse corpo para os dois eixos e . Neste caso temos um perfil sendo assim, temos os momentos de inércia tabelados:
Passo 3
Para calcular o ângulo que a linha neutra faz com o plano horizontal devemos utilizar a equação:
Resposta
Exercícios de Livros Relacionados
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.