Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 28
Montanhas-russas são projetadas de maneira que os passageiros não sintam uma força normal que seja maior do que 3,5 vezes seu peso contra o assento do carrinho. Determine o menor raio de curvatura da pista no seu ponto mais baixo se o carrinho tem velocidade de 1,5 m/s no pico da descida. Despreze o atrito.
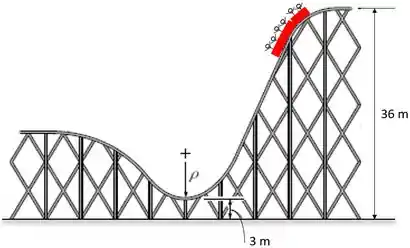
Passo 1
O enunciado nos dá a seguinte informação:
Velocidade do carrinho no pico da descida: m/s;
Além disso, ele também nos dias que a força normal não deve ser maior que 3,5 vezes o peso do passageiro, logo
Devemos determinar o raio de curvatura da pista no seu ponto mais baixo para quando o carrinho tenha velocidade de 1,5 m/s no pico da descida.
Passo 2
Utilizaremos o princípio do trabalho e energia para encontrar o valor da veloscidade do carrinho no ponto mais baixo da descida.
Temos que
onde
Substituindo esses valores na equação inicial, obtemos
Passo 3
Agora que sabemos a velocidade no ponto mais baixo, podemos aplicar a equação do movimento para descobrir o raio de curvatura.
Temos que
E que
Logo,
No ponto mais baixo da pista, temos