Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 94
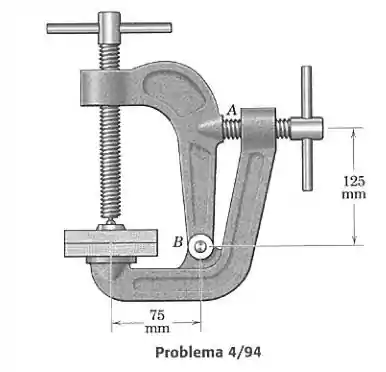
A morsa com dois atuadores mostrada na figura é usada para dar uma força de aperto adicional quando os parafusos são apertados. Se o parafuso vertical é apertado para produzir uma força de aperto de 3 kN e então o parafuso horizontal é apertado até que a força no parafuso em seja duplicada, encontra a reação total no pino em .
Passo 1
Primeiro devemos decidir quais corpos vamos isolar para satisfazer as equações de equilíbrio. Na parte mostrada na figura atuam a força do parafuso vertical, do parafuso horizontal e a reação em :
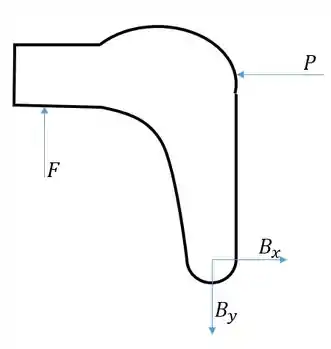
O problema diz que primeiro , e depois é dobrado. Vamos então calcular quanto era inicialmente, e depois ver quanto valem e depois, quando foram dobrados. Aí sim tentaremos achar e , para a segunda situação.
Passo 2
Se , achamos diretamente através do momento em torno de :
Então, na segunda situação e são dobrados, portanto irão valer:
Passo 3
Achamos e fazendo o equilíbrio das forças verticais e horizontais:
Agora calculamos o módulo: