Determine a força suportada por cada nó da treliça carregada.
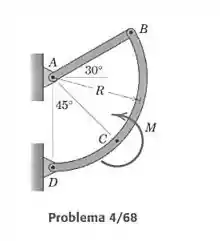
Passo 1
Olá, tudo bem? Vem comigo que vou te ajudar a resolver essa atividade.
A partir da treliça dada no problema, nos é pedido para determinar as reações no apoio de pino e . Desenhe o diagrama do corpo livre.
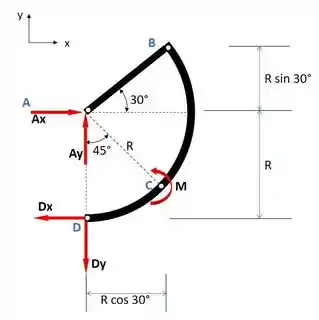
Para resolver o problema, nós iremos separar em duas partes, então iremos aplicar equações de equilíbrio:
Passo 2
Vamos isolar e desenhar o diagrama de corpo livre do membro .
Aqui, nós iremos resolver e usando equações e substituições.
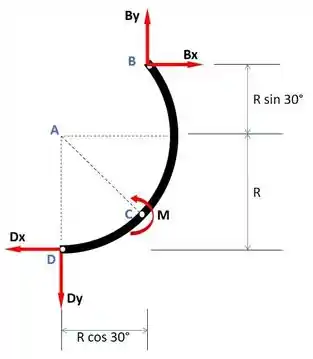
Aplicando a equação de equilíbrio, usando sobre o ponto , nós podemos obter a primeira equação de e
Passo 3
Agora, vamos isolar e desenhar o diagrama de corpo livre de . Assim também teremos equações para .
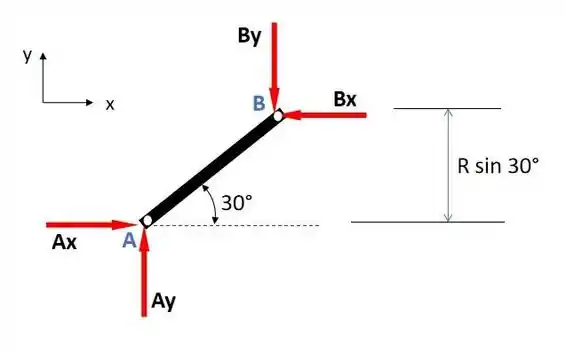
Aplicando as equações de equilíbrio, usando a equação sobre o ponto , nós poderemos encontrar as segundas equações para :
Agora iremos resolver para :
Substituindo para encontrar
Passo 4
Aplicando equações de equilíbrio, usando a equação , podemos resolver para :
Aplicando equações de equilíbrio, usando a equação , podemos resolver para :
Agora vamos analisar . Aplicando equações de equilíbrio, usando a equação , podemos resolver para :
Finalmente, aplicando as equações do equilíbrio, podemos encontrar :