Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 169
Mostrar que: (a) Se uma força vertical é aplicada no ponto da seção mostrada, a equação do eixo neutro é
Onde e , expressam os raios de giração da seção transversal em relação ao eixo e no eixo , respectivamente; (b) Se uma força vertical é aplicada em qualquer ponto localizado sobre a linha , a tensão no ponto será nula.
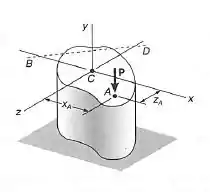
Passo 1
(a) Vamos pensar assim: se temos um ponto na seção, onde a tensão é nula, esse ponto está na linha neutra da seção. Vamos dar coordenadas genéricas para :
Agora a gente lembra que para esses eixos, a equação da tensão normal em um ponto para uma seção com uma força pontual aplicada é:
Lembrando que o sinal de menos fica no termo com o momento que causa compressão na parte positiva dos eixos.
Maasss a tensão em a gente disse que é nula porque ele está na linha neutra:
Agora a gente tem uma equação onde as únicas variáveis são e , que representa o conjunto de pontos onde , ou seja, ela representa a linha neutra.
Bora partir dela para chegar na equação do enunciado!
Passo 2
Vamos calcular os esforços internos no centroide da seção, causados por . Temos essas componentes:
- Força axial entrando na seção:
- Momentos, de acordo com os eixos coordenados:
Passo 3
Vamos substituir essas coisas na fórmulinha:
Maas, aqui a gente lembra da definição de raio de giração:
Por ter colocado aquele termo em evidência, a gente vê esses raios aparecem na nossa equação:
Uhul! Chegamos na equação do enunciado!
Passo 4
(b) Vamos achar a expressão para tensão causada em pela força , sabendo que ela está sendo aplicada no ponto que satisfaz:
E provar que essa tensão vale zero. Bora!
Passo 5
A gente vai usar a mesma fórmulinha, mas no ponto :
Vamos calcular os esforços internos no centroide da seção, causados por , que está sendo aplicada em . Temos essas componentes:
- Força axial entrando na seção:
- Momentos, de acordo com os eixos coordenados:
Passo 6
Agora vamos jogar essas coisas na fórmulinha:
Mas a gente sabe que para e , vale:
Então:
E isso é o que ele pede para provar! Arrasamos!
Resposta
Prova nos passos