Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas Revisão - Ex. 208

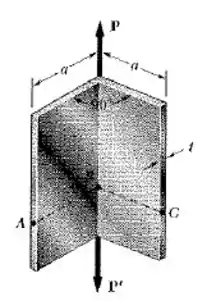
O perfilm mostrado é formado pela flexão de uma placa fina de aço. Considerando que a espessura t é pequena quando comparada ao comprimento a dos lados do perfil, determine a tensão (a) no ponto A, (b) no ponto B e (c) no ponto C.

Passo 1

Calculando inicialmente o momento de inércia referente ao centroide

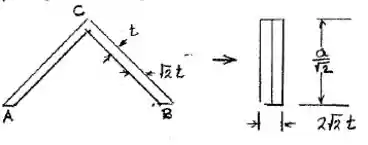
Observe que o momento de inércia será então dado por

I = 1 12 2 2 t a 2 3 = 1 12 t a 3

Passo 2

Nós teremos para área

A = 2 2 t a 2 = 2 a t

E c será a 2 2

Passo 3

Com isso podemos começar a calcular as tensões em A, B e C.

σ A = P A - P e c I = P 2 a t - P a 2 2 a 2 2 12 t a 3 = - P 2 a t

σ B = P A + P e c I = P 2 a t - P a 2 a 2 12 t a 3 = 2 P a t

Agora, observa que pra c, teremos as tensões iguais a A, logo

σ A = σ C = - P 2 a t

Concluímos

Resposta

a )   2 P a t

b )   - P 2 a t

c ) - P 2 a t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas forças P podem ser aplicadas separadamente ou ao mesmo tempo a uma placa que está soldada a uma barra circular cheia de raio r. Determine a maior tensão de compressão na barra circular.Quando amb
Sabendo que a tensão admissível na seção ABD é de 80M p a , determine a máxima intensidade da força vertical P a ser aplicada ao suporte mostrado.
Um pequeno poste de madeira suporta a carga axial de 6 kip conforme mostrado. Determine a tensão no ponto A quando: b = 0 b = 1,5i n b = 3,0i n
Podem ser aplicados até três forças axiais, cada uma da intensidade P = 50 k N , à extremidade de um perfil de aço laminado W 200 x 31,3 . Determine a tensão no ponto A.Para o carregamento mostrado,Se
Partes de 12,7 x 12,7m m de uma barra de seção quadrada foram dobradas para formar os dois componentes de maquina abaixo. Sabendo que a tensão admissível é de 103,4M p a , determine a máxima carga que