Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas Revisão - Ex. 207

Duas lâminas de latão são firmemente unidas a um perfil extrudado de alumínio, como mostrado. Usando os dados abaixo, determinar o maior momento fletor permissível, quando o membro composto é curvado em torno de um eixo horizontal.

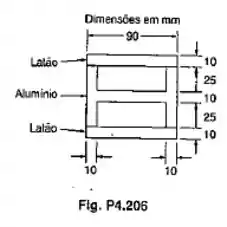
Passo 1

Do enunciado mós temos que

E a l = 70   G P a

E l = 105   G P a

Como queremos que o alumpinio diminua, teremos então para n

n = E l E a l = 105 70 = 1,5

Temos ainda que

τ a l = 100   M P a  

τ l = 160   M P a

Passo 2

Para o cálculo do momento de inércia vamos então dividir em 3 regiões, onde o momento total será dado por

I t o t = I 1 + 2 I 2 - 2 I 3

Onda cada um desses momentos é dado por

I 1,2 , 3 = h 1,2 , 3 × b 1,2 , 3 3 12 + A 1,2 , 3 d 1,2 , 3 2

I 1 = 0,06 × 0,09 3 12 + 0 = 3,645 × 10 - 6 m 4

Observe que a segunda parcela do momento de inércia foi zero já que é nula a distancia do y - que entra na conta.

I 2 = 0,1 × 0 , 0 1 35 3 12 + 0 = 2,05 × 10 - 6 m 4

I 3 = 0 , 0 25 × 0,0 7 3 12 + 0 = 7,146 × 10 - 7 m 4

O I t o t será então

I t o t = 3,645 × 10 - 6 + 2 × 2,05 × 10 - 6 - 2 × 0 , 7 146 × 10 - 6 = 9,17 × 10 - 6 m 4

Passo 3

Para o maior momento fletor vamos ter duas opções. Nossa primeira opção é então

τ a l = M c a l I t o t

Isolando o M

M = 100 ×   10 6 × 9,17 × 10 - 6 0,03 = 30,56   k N . m

Vamos ver se o latão aguenta esse momento. Para o latão não podemos esquecer de usar nosso n calculado la no comecinho da questão

τ l = n M c l I t o t = 1,5 × 30,56 × 10 3 × 0,04 9,17 × 10 - 6 = 200   M P a

200   M P a > 160   M P a

Opa, passa do valor admissível! Então vamos fazer o mesmo agora, mas calculando o momento para o latão inicialmente.

τ l = n M c l I t o t

Isolando o M

M = 160 × 10 6 × 9,17 × 10 - 6 1,5 × 0,04 = 24,45   k N . m

Aplicando esse momento no alimpinio

τ a l = M c a l I = 24,45 × 10 3 × 0,03 9,17 × 10 - 6 = 80   M P a

80 M P a < 100   M P a

Maravilha! 80MPa é aceitável

Resposta

M = 24,45   k N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga curva e o carregamento indicados na figura, determine a tensão no (a) ponto A e (b) ponto B.
Para o gancho de guindaste mostrado na figura, determine a maior tensão de tração na seção a-a.
Sabendo que o componente de máquina mostrado na figura tem uma seção transversal trapezoidal com a = 88,9m m e b = 63,5m m , determine a tensão no (a) ponto A e (b) ponto B.
Usando a equação (4.66), determine a expressão para R dada na Fig. 4.61 para uma seção transversal triangular.
Usando a equação (4.66), determine a expressão para R dada na Fig. 4.61 para uma seção transversal circular.