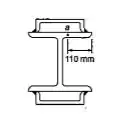
A viga composta é feita pela soldagem de perfis de aço laminado C200x17,1, as abas de um perfil de aço laminado W250x80, como mostrado. Sabendo-se que a viga é submetida a uma força cortante vertical de 200kN, determinar a força cisalhante horizontal por unidade de comprimento em cada solda.

Vamos pegar os dados dos perfis, você pode encontra-lo no final do livro:

Perfil C200X17,1:

Perfil W250X80:

, , mm

Precisamos calcular o momento de inércia, nesse caso temos o momento de inércia do perfil W e do C, porém pro C precisaremos usar o teorema dos eixos paralelos, o centro do perfil C tem a distância do centro da viga composta dada por:

Note que o perfil C está girado e invertido, então o centro está na direção y e deve ser subtraído da largura bf.

Pelo teorema dos eixos paralelos temos:

E com isso a inércia total será:

Onde é a inércia do perfil W.