Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 113
A velocidade de um tambor de freio mostrado na figura é controlada por uma cinta fixada a uma cinta fixada a uma barra de controle . A força de intensidade de é aplicada na barra de controle em . Determine a intensidade do torque que está sendo aplicado ao tambor, sabendo que o coeficiente de atrito cinético entre a cinta e o tambor é , que e que o tambor está rodando a uma velocidade constante no sentindo anti-horário, no sentido horário.
Passo 1
Bom galera, começamos fazendo um diagraminha:
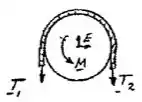
Com isso temos:
Passo 2
Show de bola, vamos analisar a barra de controle:
Agora, substituindo :
E assim:
Passo 3
Analisando agora o momento do tambor:
Passo 4
Por fim, a gente faz o mesmo para o sentido horário, analisando a barra de controle:
E:
E o momento do tambor fica:
Resposta
Exercícios de Livros Relacionados
Calcule a magnitude do binário M no sentido horário necessário para girar o cilindro de 50k g no bloco de suporte mostrado. O coeficiente de atrito cinético é 0,30 .
O bloco retangular homogêneo de massa m repousa sobre o plano inclinado que é articulado em torno de um eixo horizontal através de O . Se o coeficiente de atrito estático entre o bloco e o plano for μ
A placa semicircular de 5k g gira em torno de um rolamento fixo em O que pode exercer um momento de atrito máximo de 1,2N m na placa. A força horizontal P é aplicada a uma corda enrolada em torno da p
Determine o coeficiente de atrito estático mínimo entre a bobina uniforme de 50 kg e a parede de modo que ela não deslize.
Determine a força P máxima que pode ser aplicada sem causar o movimento da caixa de 100 kg com centro de gravidade em G . O coeficiente de atrito estático no piso é μ s = 0 , 4 .