Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 150

(a) Determine o vão horizontal máximo permitido para um cabo uniforme de peso por unidade de comprimente w se a tração no cabo não exceder um valor dado T m (b) Usando o resultado da parte a , determine o vão máximo de um cabo de aço para o qual w = 3,75   N / m e T m = 36   k N .

Passo 1

Bom galera, vamos fazer um diagraminha de corpo livre, só pra facilitar nossa vida:

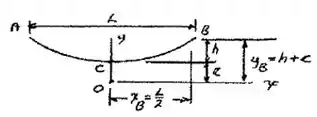
Com isso, de cara a gente já tem algumas informações:

Tração máxima:

T m = w y B

→ T m = w c cosh ⁡ x B c

→ T m = w x B 1 x B c cosh ⁡ x B c

Passo 2

Show de bola, nós podemos encontrar x B c , para quando T m for mínimo:

d T m d x B c = w x B 1 x B c sinh ⁡ x B c - 1 x B c 2 cosh ⁡ x B c = 0

E a gente continua desenvolvendo:

→ sinh ⁡ x B c cos h ⁡ x B c = 1 x B c

→ tanh ⁡ x B c = c x B

Resolvendo por tentativa e erro, encontramos:

c x B = 1 , 200

Passo 3

Calma, tá quase acabando. Vamos usar também a equação 7.16 :

s B = c sin h ⁡ x B c

→ s B = c sinh ⁡ 1 , 200

→ s B c = 1,509

Então, usamos a equação 7.17 :

y B 2 - s B 2 = c 2

→ y B 2 = c 2 1 + s B c 2 = c 2 1 + 1,509 2

→ y B = 1,810 c

E a equação 7.18 :

T m = w y B

→ T m = 1,810 w c

→ c = T m 1,810 w

Passo 4

Por fim, a gente pega a equação que já tínhamos encontrado:

c x B = 1,200

→ x B = c 1,200

E substituímos c :

→ x B = T m 1,810 w 1,200 = 0,6630 T m w

E sabemos que L é o dobro de x B , logo:

L = 1,326 T m w

Agora, para w = 3,75   N / m e T m = 36   k N :

L = 1,326 3,75 36

→ L = 0,1381   m

Resposta

L = 1,326 T m w

L = 0,1381   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga A B , que esta disposta sobre o solo, sustenta a carga parabólica mostrada na figura. Considerando que a reação para cima do solo é uniformemente distribuída, a escreva as equações das curvas d
Para a viga e o carregamento mostrados nas figuras, a deduza as equações das curvas de esforço cortante e momento fletor, b determine a intensidade e a localização do máximo momento fletor.
Para a viga e o carregamento mostrados nas figuras, a deduza as equações das curvas de esforço cortante e momento fletor, b determine a intensidade e a localização do máximo momento fletor.
Para a viga e o carregamento mostrados nas figuras, a deduza as equações das curvas de esforço cortante e momento fletor, b determine a intensidade e a localização do máximo momento fletor.
A viga A B , que está sujeita ao carregamento uniformemente distribuído mostrado na figura e a duas forças desconhecidas P e Q . Sabendo que foi experimentalmente determinado que o momento fletor é +