Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas de Revisão - Ex. 197
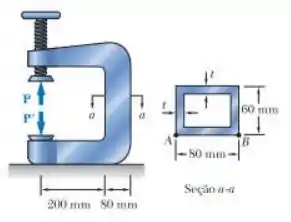
A parte vertical da prensa mostrada na figura consiste em um tubo retangular com espessura de parede . Sabendo que a prensa foi usada para prender blocos de madeira que estavam sendo colados, com uma força , determine a tensão no ponto e ponto .
Passo 1
Fala aí galera, beleza? Bora resolver mais um exercício.
Neste problema, temos que encontrar a tensão nos pontos e .
Primeiro, vamos encontrar o momento fletor, que é dado pelo produto da força que o enunciado nos deu, de , pela distância entre o eixo que passa pelo centroide e a linha linha neutra da seção transversal. Esta distância é dada por:
Com isso, podemos encontrar o momento fletor. Logo:
Passo 2
Depois, temos que calcular a área da seção transversal, ela é dada pela subtração da área do retângulo maior pela área do retângulo menor. Como o problema nos fala que a parede tem a espessura de , temos:
Em seguida, vamos calcular o momento de inércia para esta seção. Assim como a área, ele é dado pela subtração dos momentos de inercia:
Onde é o momento de inercia para retângulo maior e para o menor. E como estamos falando de retângulos, os momentos de inercia vão ser dados por:
Passo 3
Agora que a gente tem o momento fletor, a força e a área da seção, precisamos encontrar a última variável da qual a tensão depende, a distância do centroide em relação ao eixo principal de inercia da seção. Portanto:
Com isso, podemos calcular as tensões. Para o ponto , temos:
E para o ponto , temos:
É isso, galera!!! Bora fazer mais questões.