Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 144a

O tubo mostrado na figura tem parede com espessura constante de 12mm. Para o carregamento dado, determine.

  1. A tensão nos pontos A e B.

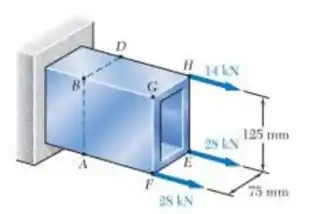
Passo 1

Para determinação de tensões em elementos que estão sujeitos a momentos fletores inclinados, ou ainda, momentos fletores oblíquos, ou momentos fletores assimétricos, temos a seguinte fórmula:

σ = P A - M z y I z z + M y z I y y

Em que:

M z = p a r c e l a   d o   m o m e n t o   n a   d i r e ç ã o   z

M y = p a r c e l a   d o   m o m e n t o   n a   d i r e ç ã o   x

y   e   z = c o o r d e n a d a s   n o   p o n t o   e m   q u e   s e   d e s e j a   s a b e r   a   t e n s ã o   e m   c a d a   d i r e ç ã o

I z z = m o m e n t o   d e   i n é r c i a   e m   t o r n o   d e   z

I y y = m o m e n t o   d e   i n é r c i a   e m   t o r n o   d e   y

Precisamos então definir os carregamentos que agem na nossa seção, para isso precisamos ver a nossa seção, com isso teremos que:

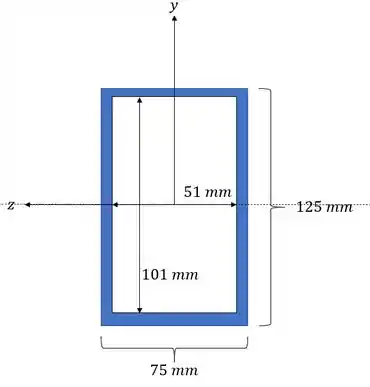
Passo 2

Se temos a seção, podemos pensar os carregamentos que agem, sendo assim podemos pensar o seguinte:

  • Carga P

    • P = 14 + 28 + 28 = 70   k N = 70000 N

  • Carga de momento na direção y

    • Para termos os momentos na direção y, precisamos das distancia na direção Z, e com isso podemos analisar as cargas que agem na seção.

    M y = 28   .   37,5 - 28   .   37,5 - 14   .   37,5 = - 525   k N m m = - 525000   N m m

  • Carga de momento na direção Z

Para termos os momentos na direção Z, precisamos das distancia na direção Y, e com isso podemos analisar as cargas que agem na seção.

M z = 28   .   62,5 + 28   .   62,5 - 14   .   62,5 = 2625   k N m m = 2625000   N m m

Passo 3

Os dados de seção que podemos analisar são dados por:

A = 125   .   75 - 101   .     51 = 4224   m m 2

I z z = 75   .   125 3 12 - 51   .   101 3 12 = 7828252   m m 4

I y y = 125   .   75 3 12 - 101   .   51 3 12 = 3278052   m m 4

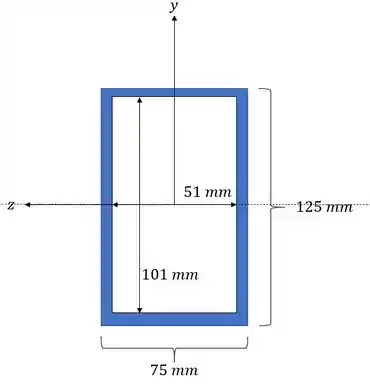
Passo 4

E agora precisamos determinar os valores de y e z de cada ponto que desejamos determinar as tensões, sendo assim, teremos que:

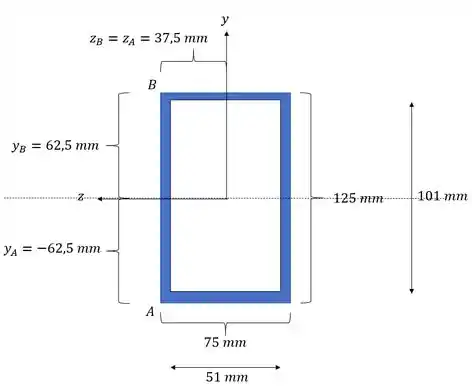
Substituindo a tensão, teremos que:

σ A = P A - M z y A I z z + M y z A I y y

σ A = 70000 N 4224   m m 2 - 2625000   N m m .   - 62,5 m m 7828252   [ m m 4 ] + - 525000   [ N m m ]   .     37,5 m m 3278052   [ m m 4 ]

σ A = 31,5   M P a

σ B = P A - M z y B I z z + M y z B I y y

σ B = 70000 N 4224   m m 2 - 2625000   N m m .   62,5 m m 7828252   [ m m 4 ] + - 525000   [ N m m ]   .     37,5 m m 3278052   [ m m 4 ]

σ B = - 10,39   M P a

Resposta

σ A = 31,5   M P a

σ B = - 10,39   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a localização do centro de cisalhamento O de viga de paredes finas de espessuras constante que possui a seção transversal mostrada.
Uma viga de paredes finas com espessuras uniforme tem a seção transversal mostrada. Determine a dimensão b de modo que o centro de cisalhamento O da seção transversal fique localizado no ponto indicad
A viga composta mostrada é feita soldando perfis U laminados de aço C 200x17,1 as mesas do perfil de aço laminados de mesas largas W250x80 . Sabendo que a viga é submetida a uma força cortante de 200k
Resolva o Problema 4.150 considerando que o momento M 0 age em um plano horizontal.
Resolva o Problema 4.152 considerando que o momento M 0 atua em um plano horizontal.