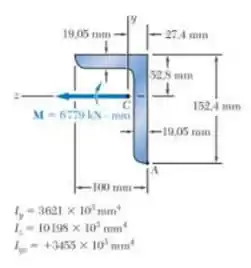
O momento M atua em um plano vertical e é aplicado a uma viga orientada, conforme mostra a figura. Determine a tensão no ponto A.
Passo 1
Fala galerinha, agora vamos entrar em um novo tipo de questão, ainda vamos continuar com os mesmos conceitos que aprendemos até agora, mas com coordenadas diferentes, isso vai acontecer porque a nossa LN não vai ser mais centralizada na vertical ou na horizontal como estamos acostumados, agora ela vai ficar na diagonal, e isso é um novo conceito para nós, pois mudará as nossas equações, por isso, olhando a nossa seção, temos que a nossa LN pode girar do seguinte modo:
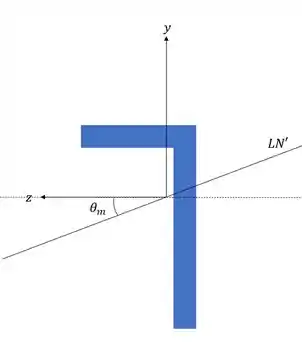
Perceba que em pontilhado eu coloquei a LN “original” que chutaríamos para a nossa seção, e em linha cheia está a nossa LN’ que é a que de fato atua na nossa seção.
Até aqui tudo bem certo? Porém, pense no seguinte, nos calculávamos tudo com relação a LN certo? Como calcular com relação a essa nova? É ai que vai entrar o que precisamos. Lembra do nosso velho amigo círculo de mohr? Que nos ajudava a achar tensões máximas? Ele agora vai nos ajudar a achar inercias máximas, e a nossa inércia máxima vai ser exatamente a que atua na nossa LN, então vamos lá, como montar esse circulo de mohr para inércias?
- Passo 1 – Definido as coordenadas
- MOMENTOS FLETORES
As nossas coordenadas vão ser dadas por:
Assim teremos que:
Lembrando que todos são multiplicados por , mas pra facilitar o cálculo me preocupei apenas com os valores principais. Lembrando das nossas fórmulas do círculo de mohr, podemos determinar as nossas inércias pela seguinte equação:
E as inércias máximas e mínimas serão dadas por:
E como temos que lembrar, precisamos multiplicar tudo por .
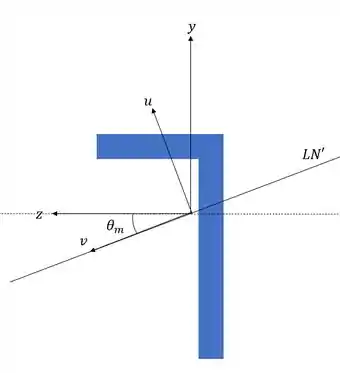
E o que são ? São as novas coordenadas do nosso sistema, assim, temos que:
Passo 2
Agora que já temos as inércias, precisamos determinar o ângulo para podermos determinar as coordenadas, e sabe como podemos determinar isso? Lembra da nossa formulazinha do círculo de mohr? Que calculava ângulo? Isso mesmo, vamos usar ela mesmo, assim temos que:
Agora que temos o ângulo, podemos analisar tanto o valor de momento quanto os correspondestes de nas coordenadas , assim, teremos que:
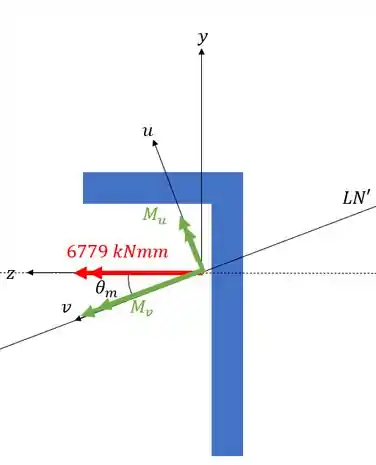


Passo 2
Agora só precisamos lembrar que a determinação da tensão é dada pela seguinte equação adaptada:
Assim temos que: