Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 121
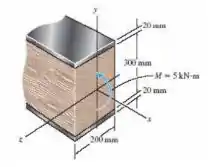
As partes superior e inferior da viga de madeira são reforçadas com tiras de aço, como mostra a figura. Determine a tensão de flexão máxima desenvolvida na madeira e no aço se a viga for submetida a um momento fletor M = 5 kN.m. Trace um rascunho da distribuição de tensão que age na seção transversal. Considere Emad = 11 GPa, Eaço = 200 GPa.
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? A nossa questão de hoje nos traz uma viga composta por dois materiais diferentes, mas vou te explicar direitinho.
Os materiais que compõem são a madeira e o aço, e ele nos pede para calcular as duas tensões de flexão máximas (tanto para a madeira quanto para o aço) para um momento fletor igual a 5 kN.m.
Viu?? Ela só tem cara de malvada, esse tipo de questão tem um passo a passo. Só seguir ele que dá bom. Vem comigo!!
Passo 2
A primeira coisa que precisamos achar é a relação entre os coeficientes e .
Como a gente deixou o aço no denominador, nossa estratégia vai ser trocar a parte de madeira por uma equivalente de aço.
A gente pode multiplicar o comprimento da madeira por esse valor e achar um comprimento equivalente em aço:
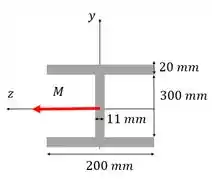
Nossa nova viga equivalente toda em aço é:
Passo 3
Agora que já temos nossas dimensões, podemos calcular nossos momentos máximos da viga. Para isso, vamos calcular primeiro o nosso I, para só depois substituir na nossa formulinha.
A tensão máxima no aço vai estar no ponto mais da distante da linha neutra (nesse caso, ela passa pelo centroide) que pertence a região que inicialmente era de aço. Então
Logo:
A tensão máxima na madeira vai estar no ponto mais da distante da linha neutra (nesse caso, ela passa pelo centroide) que pertence a região que inicialmente era de madeira. Então
Repara que a gente multiplicou nossa fórmula comum pelo na hora de calcular a tensão de madeira, porque foi nesse material que a gente fez a transformação, ok?
Passo 4
Como já temos nosso resultado, falta só esboçar!! A tensão é linear para os dois materiais. Ela vai zerar na linha neutra.
Mas repara que a tensão do aço vai ser máxima em e mínima no encontro com a parte de madeira.
E a tensão máxima da madeira acontece nesse encontro, mas como o do aço é muito maior, a tensão máxima da madeira vai ser bem menor do que a mínima tensão na parte de aço.
Lembrando que na parte de cima vamos ter compressão e na parte de baixo tração, por causa da orientação do momento.
Logo, nosso desenho fica
