Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 103

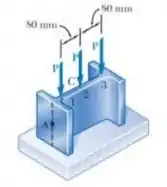
Podem ser aplicados até três forças axiais, cada uma da intensidade P = 50 k N , à extremidade de um perfil de aço laminado W 200 x 31,3 . Determine a tensão no ponto A.

  1. Para o carregamento mostrado,
  2. Se as forças aplicadas ao ponto 1 e 2 somente.

Passo 1

Fala galerinha, nosso objetivo é determinar a tensão nos pontos A e B, certo? E para isso temos 2 cargas decentralizadas e uma centralizada, certo? Então vamos montar a nossa fórmula com base nas distâncias dadas.

Para isso precisamos lembrar que a nossa fórmula de tensão é dada por.

σ x = - P A - M y I

Antes de qualquer coisa, precisamos levar as nossas cargas para o centro da seção.

As cargas P’s podemos levar diretamente, mas lembra que temos 3 cargas P’s, que vamos chamar de P 1 ,     P 2 e P 3 :

P = P 1 + P 2 + P 3

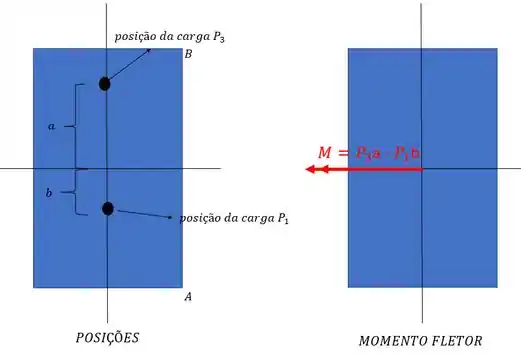
E como essas cargas são deslocadas com relação ao centro da seção que se deseja determinar as tensões, teremos o seguinte momento fletor gerado, considerando uma distância arbitrária que vamos chamar de a   e   b .

M = P 3 a - P 1 b

Passo 2

Vamos definir o momento de inércia, a área e y, assim teremos que:

  • I

    • Esse tiramos da tabela no fim do livro:

    I = 31,3 × 10 6   m m 4

  • Área da seção

    • Esse tiramos da tabela no fim do livro:

    A = 3970   m m 2

  • y - positivo e negativo

Esse tiramos da tabela no fim do livro:

y A = - 210 2 = - 105   m m

Substituondo na nossa equação temos que:

σ = P A - M y I

Substituindo o momento e a carga P tem-se que:

σ = - P 1 - P 2 - P 3 A - ( P 1 a - P 2 b ) y I

Para o item A) temos que:

P 1 = 50   k N

P 2 = 50   k N

P 3 = 50   k N

a = 80   m m

b = 80   m m

I = 31,3 × 10 6   m m 4

A = 3970   m m 2

y A = - 105   m m

Substituindo teremos que:

σ A = - P 1 - P 2 - P 3 A - ( P 1 a - P 2 b ) y I

σ A = - 50 - 50 - 50 [ k N ] 3970   [ m m 2 ] - 50 × 80 - 50 × 80 k N - 105 m m 31,3 × 10 6   m m 4 = - 0,0378 k N m m 2

σ A = - 37,8   M P a

Para o item B) temos que:

P 1 = 50   k N

P 2 = 50   k N

P 3 = 0   k N

a = 80   m m

b = 30   m m

I = 31,3 × 10 6   m m 4

A = 3970   m m 2

y A = - 105   m m

Substituindo teremos que:

σ A = - P 1 - P 2 - P 3 A - ( P 1 a - P 2 b ) y I

σ A = - 50 - 50 - 0 [ k N ] 3970   [ m m 2 ] - 0 × 80 - 50 × 80 k N - 105 m m 31,3 × 10 6   m m 4 = - 0,0386 k N m m 2

σ A = - 38,6 M P a

Resposta

  1. σ A = - 37,8   M P a

  2. σ A = - 38,6   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O momento M atua em um plano vertical e é aplicado a uma viga orientada conforme mostra a figura. Determine:O ângulo que a linha neutra forma com a horizontal e.A tensão de tração máxima na viga.
O momento M atua em um plano vertical e é aplicado a uma viga orientada, conforme mostra a figura. Determine a tensão no ponto A.
O momento M atua em um plano vertical e é aplicado a uma viga orientada, conforme mostra a figura. Determine a tensão no ponto A.
O tubo mostrado na figura tem parede com espessura constante de 12mm. Para o carregamento dado, determine.A tensão nos pontos A e B.
O momento M atua em um plano vertical e é aplicado a uma viga orientada, conforme mostra a figura. Determine a tensão no ponto A.