Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 147

Sabendo que a = 1,25   i n , determine o maior valor de P que pode ser aplicado se exceder as tensões admissíveis a seguir:

σ t r a ç ã o = 10   k s i

σ c o m p r e s s ã o = 1 8   k s i

Passo 1

Para determinação de tensões em elementos que estão sujeitos a momentos fletores inclinados, ou ainda, momentos fletores oblíquos, ou momentos fletores assimétricos, temos a seguinte fórmula:

σ = P A - M z y I z z + M y z I y y

Em que:

M z = p a r c e l a   d o   m o m e n t o   n a   d i r e ç ã o   z

M y = p a r c e l a   d o   m o m e n t o   n a   d i r e ç ã o   x

y   e   z = c o o r d e n a d a s   n o   p o n t o   e m   q u e   s e   d e s e j a   s a b e r   a   t e n s ã o   e m   c a d a   d i r e ç ã o

I z z = m o m e n t o   d e   i n é r c i a   e m   t o r n o   d e   z

I y y = m o m e n t o   d e   i n é r c i a   e m   t o r n o   d e   y

Precisamos então definir os carregamentos que agem na nossa seção, para isso precisamos ver a nossa seção, com isso teremos que:

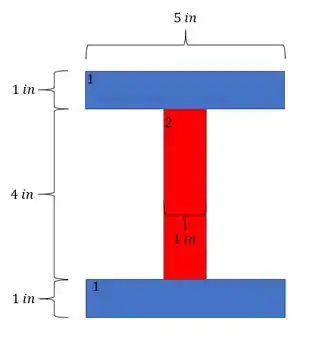
Passo 2

Podemos levar a nossa carga P para o centro da nossa LN, assim teremos que:

  • Carga P

    • P = c a r g a   d i r e t o   n o   c e n t r o   d a   s e ç ã o .

  • Carga de momento na direção y

    • Para termos os momentos na direção y, precisamos das distancia na direção Z, e com isso podemos analisar as cargas que agem na seção.

    M y = P a

  • Carga de momento na direção Z

    • Para termos os momentos na direção Z, precisamos das distancia na direção Y, e com isso podemos analisar as cargas que agem na seção.

    M z = 2,5 P

    Passo 3

    Os dados de seção que podemos analisar são dados por:

    A = 2 × 1 × 5 + 4 × 1 = 14   i n 2

    I z z = 2 × 5 × 1 3 12 + 5 × 1 × 2,5 2 + 1 × 4 3 12 = 68,67   i n 4

    I y y = 2 1 × 5 3 12 + 4 × 1 3 12 = 21,17   i n 4

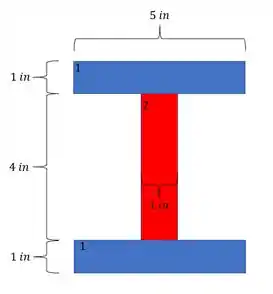
    Passo 4

    Como queremos a máxima tensão de compressão, precisamos do ponto em que ocorre compressão dupla, assim teremos que:

  • Compressão

  • Tração

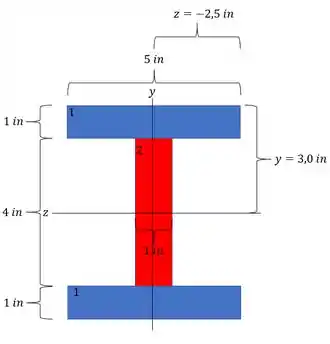
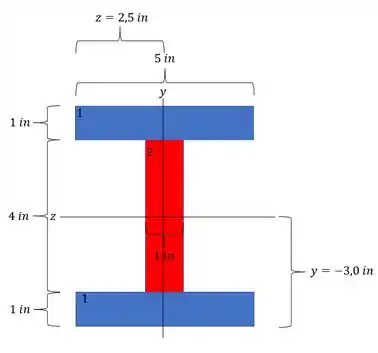
    • Passo 5

    Assim a nossa tensão vai ser dada por:

  • Compressão

    • σ = P A - M z y I z z + M y z I y y

    σ = - P 14 - 2,5   .     P   .   3 68,67 + P a   .     ( - 2,5 ) 21,17

    Sabemos que a = 1,25   i n

    a = 1,25   i n

    E assim podemos usar a seguinte tensão:

    σ = - 18   k s i

    - 18 = - P 14 - 2,5   .     P   .   3 68,67 + P   .   1,25   .     ( - 2,5 ) 21,17

    P = 54,8   k i p

  • Tração

σ = P A - M z y I z z + M y z I y y

σ = - P 14 - 2,5   .     P   .   ( - 3 ) 68,67 + P a   .     ( 2,5 ) 21,17

Sabemos que a = 1,25   i n

a = 1,25   i n

E assim podemos usar a seguinte tensão:

σ = 10   k s i

1 0 = - P 14 - 2,5   .     P   .   ( - 3 ) 68,67 + P 1,25   .     ( 2,5 ) 21,17

P = 53,9   k i p

Precisamos escolher a menor força para termos a maior segurança, assim, precisamos de:

P = 53,9   k i p

Resposta

P = 53,9   k i p

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga de seção transversal assimétrica está submetida a um momento M 0 atuando no plano vertical x y . Mostre que a tensão no ponto A, de coordenadas y e z , é σ A = - y I y - z I y z I y I z - I y
A barra curva mostrada tem seção transversal de 40 x 60 mm e raio interno r 1 = 15m m . Para o carregamento mostrado, determine as maiores tensões de tração e compressão.
Resolva o Problema 4.167 considerando que β = 60 ° .
As chapas de ligação de aço com a seção transversal mostrada na figura estão disponíveis com diferentes ângulos centrais β . Sabendo que a tensão admissível é de 82,7 MPa, determine a maior força P qu
Para a barra curva e o carregamento mostrado, determine o erro percentual introduzido na computação da tensão máxima admitindo que a barra é reta. Considere o caso em que (a) r 1 = 20m m , (b) r 1 = 2