Uma polia dupla está presa a um bloco deslizante por um pino em A. A polia interna, de de raio, está rigidamente presa à polia externa, de raio de . Sabendo que cada uma das cordas é puxada com velocidade constante do modo mostrado na figura, determine (a) o centro instantâneo de rotação da polia dupla, (b) a velocidade do bloco deslizante e (c) o número de milímetros de corda enrolada ou desenrolada sobre cada polia por segundo.
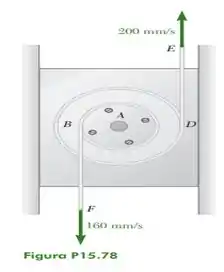
Passo 1
Questão 78 agora, meus chapas!
Bom! Vamos começar nossa resolução, fazendo um esboço do que está acontecendo em nosso problema... A chamada representação vetorial das velocidades!
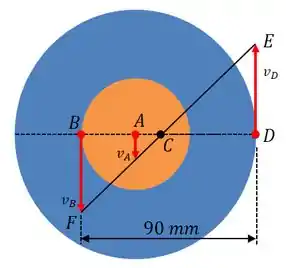
Bom! A gente tem que...
Passo 2
a) O sentido em que as duas cordas estão sendo puxados, vão fazer com que a polia gire no mesmo sentido. Sendo assim, a velocidade angular é dada por...
Sendo assim, para obter a distância , basta fazer com que...
E então, a distância entre e , , será de...
Logo, o centro instantâneo de rotação da polia dupla fica à direita de .
Passo 3
b) A velocidade do bloco deslizante, é a velocidade que representamos em nosso desenho e que pode ser facilmente obtida como...
Passo 4
c) Por fim, para obter o número de milímetros de corda enrolada ou desenrolada sobre cada polia por segundo, precisamos usar o conceito de velocidade relativa...
Fazemos isso, pois estamos analisando o movimento entre dois objetos. Para a polia maior, temos que serão deslizados um valor igual à...
Para a polia menor, por sua vez, serão deslizados...
Ou seja, está deslocando por segundo. E está deslocando por segundo!
Feshow!? Bora pra frente que atrás vem gente!
Resposta
a)
b)
c)