Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 58

15.58. No sistema biela-manivela de motor mostrado na figura, l 160 mm e b 60 mm. Sabendo que a manivela AB gira com uma velocidade angular constante de 1.000 rpm no sentido horário, determine a velocidade do pistão P e a velocidade angular da biela quando (a) 0, (b) 90°.

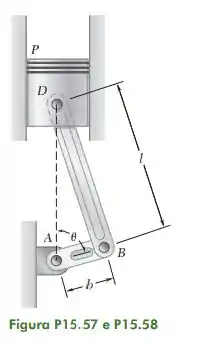
Passo 1

Vamos lá!

As informações que temos para resolver o item (a) são:

ω A B = 1000   r p m = 104,72 r a d s l = 160   m m b = 60   m m θ = 6 0 °

Podemos começar determinando a velocidade do ponto B:

v B = b ⋅ ω A B = 104,72 ⋅ 60 = 6283,2 m m s

Vamos ter o seguinte triangulo formado na imagem:

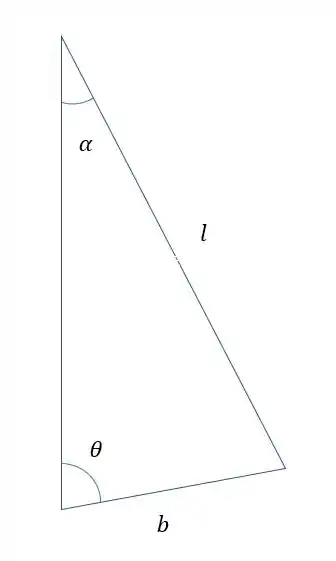
Assim podemos descobrir o valor de α , através do teorema dos senos

l sin ⁡ α = b sin ⁡ θ

α = arcsin ⁡ b α sin ⁡ θ = arcsin ⁡ 60 160 sin ⁡ 60 ° = 18,95 °

Passo 2

No segmento BD, podemos fazer

v D = v B + v D B

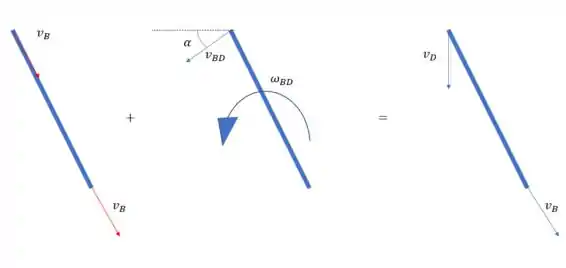
Então formamos um triangulo com os vetores.

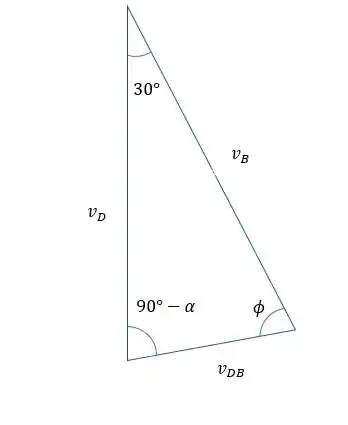
Usando novamente a lei dos senos, temos

v D sin ⁡ ϕ = v B D sin ⁡ 30   ° = v B sin ⁡ ( 90 ° - α )

Nós já conhecemos o valor de α , mas podemos calcular o valor de ϕ usando o principio que a soma dos ângulos internos do triangulo é 180°.

180 ° = 90 ° - α + ϕ + 30 °

Então

ϕ = 180 ° - 30 ° + 90 ° + α = 78,95 °

Então

v D sin ⁡ 78,95 ° = v B D sin ⁡ 30   ° = v B sin ⁡ ( 90 ° - 18,95 ° )

Passo 3

Vamos calcular v D , já que sabemos que v D = v P , basta olhar a imagem.

v D = v B sin ⁡ ϕ sin ⁡ ( 90 - α )

v D = 6,3832 sin ⁡ 78,95 sin ⁡ 90 - 18,95 = 6,52 m s

Agora vamos calcular v D B

v D B = v B sin ⁡ 30 ° sin ⁡ 90 ° - α

v D B = 6,2832 sin ⁡ 30 ° sin ⁡ 90 - 18,95 = 3,3216 m s

Com essa velocidade podemos calcular a velocidade angular

ω B D = v B D l = 3,3216 0,16 = 20,8 r a d s

Resposta

v P = 6,52 m s ω B D = 20,8 r a d s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.107. A placa quadrada está restringida dentro das ranhuras A E B . Quando θ = 30°, o ponto A está se deslocando com V A = 8 m / s . Determine a velocidade do ponto D.
16.104. Se o volante A está girando com uma velocidade angular ω A = 10 r a d s , determine a velocidade da roda B no instante mostrado.
16.105. Se a A B está girando com uma velocidade angular ω A B = 6 r a d / s , determine a velocidade do centro O da engrenagem no instante mostrado.
A viga está sujeita ao carregamento mostrado na figura. Determine a dimensão a exigida para sua seção transversal se a tensão admissível para o material for σmáx = 150 MPa.
75. No instante mostrado, o caminhão se desloca para a direita a 8m/s. Se o cano não desliza em B, determine sua velocidade angular se seu centro de massa G permanece estacionário a um observador no s