Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 178b

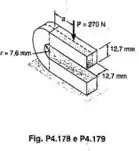
A porção curva da barra mostrada tem um raio interno de 7,6 mm. A linha de ação da força de 270 N está localizada a uma distância a do plano que contém o centro de curvatura da barra. Determinar a maior tensão de compressão quando (a) a = 0 (b) a = 30   m m

Passo 1

Beleza! A gente já resolveu tudo no item ( a ) , agora vamos resolver o item ( b ) considerando o caso em que a = 30   m m

M = 270   N   a + 13,95   m m = 11866,5   N ⋅ m m

A tensão no raio interno:

σ r 1 = σ R + M ⋅ r 1 - R A e r 1

σ r 1 = - 1,674   M P a + 11866,5     N ⋅ m m ⋅ ( 7,6   m m - 12,9266   m m ) 161,29   m m 2 ⋅ 1,0234   m m ⋅ 7,6   m m

σ r 1 = - 1,674   M P a - 50,386   M P a

σ r 1 = - 52,06   M P a

A tensão no raio externo:

σ r 2 = σ R + M ⋅ r 2 - R A e r 2

σ r 2 = - 1,674   M P a + 11866,5   ⋅ m m ⋅ ( 20,3   m m - 12,9266   m m ) 161,29   m m 2 ⋅ 1,0234   m m ⋅ 20,3   m m

σ r 2 = - 1,674   M P a + 26,112   M P a

σ r 2 = 24,438   M P a

Resposta

σ r 1 = - 52,06   M P a

σ r 2 = 24,438   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O momento M atua em um plano vertical e é aplicado a uma viga orientada conforme mostra a figura. Determine:O ângulo que a linha neutra forma com a horizontal e.A tensão de tração máxima na viga.
O momento M atua em um plano vertical e é aplicado a uma viga orientada, conforme mostra a figura. Determine a tensão no ponto A.
O momento M atua em um plano vertical e é aplicado a uma viga orientada, conforme mostra a figura. Determine a tensão no ponto A.
O tubo mostrado na figura tem parede com espessura constante de 12mm. Para o carregamento dado, determine.A tensão nos pontos A e B.
O momento M atua em um plano vertical e é aplicado a uma viga orientada, conforme mostra a figura. Determine a tensão no ponto A.