Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 58
Resolver o Prob. 4.57, considerando que é a espessura do tubo interno, feito de alumínio, e que é a espessura do tubo externo, feito de aço.
Passo 1
Queremos analisar essa viga composta. Os dados que temos são:
-
-
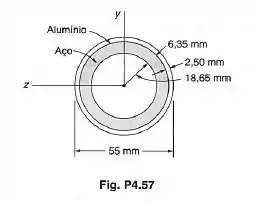
- Raio interno da parte de alumínio:
- Raio externo da parte de alumínio e interno da parte de aço:
- Raio externo da parte de aço:
- Momento fletor aplicado:
Vamos transformar a parte de aço em uma parte equivalente de alumínio. Para isso, nosso fator de transformação vai ser:
Belezinha! Agora é fazer continhas. Vem comigo!
Passo 2
a) Queremos a tensão máxima na parte de alumínio. Primeiro a gente precisa calcular o momento de inércia da seção.
Como o nosso material de referência é o alumínio, o momento de inércia da parte de alumínio fica assim:
Já o momento de inércia da parte de aço vai ter um detalhezinho a mais.
A gente não vai multiplicar o fator por nenhuma dimensão da parte de aço, porque ela é circular. Não é viável multiplicar por nenhuma dimensão que é paralela ao eixo horizontal quando a gente fala de círculos.
O que vamos fazer então? A gente pode multiplicar pelo próprio momento de inércia dessa parte. Fica assim:
O momento total fica:
Passo 3
A tensão máxima no alumínio fica:
Passo 4
b) Queremos calcular a tensão máxima na parte de aço. Agora a gente precisa usar o fator . Fica assim:
Passo 5
c) Para finalizar, a gente quer o raio de curvatura da viga. Só usar a fórmulinha:
Resposta
(a)
(b)
(c)