Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 83

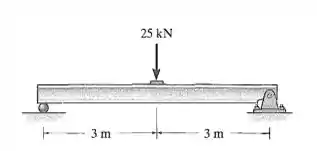
É possível que as vigas de plástico reforçado substituam as vigas de aço, pois seu peso é 1 4 destas. Utilizando a tabela do apêndice B, com σ a d m = 160 M P a   e τ a d m = 84 M P a , selecione a viga de aço de abas largas mais leve que suportará com segurança 25kN e calcule sua deflexão máxima. Se a viga fosse de plástico, E = 126 G P a ,   qual seria a deflexão máxima?

Passo 1

Fala aí galera. Vamos pra mais uma questão de resmat. O problema quer que a gente escolha uma estrutura que seja adequada para a situação. Primeiramente, sabemos que:

σ a d m = M m á x c I

I c = M m á x σ a d m

Logo, esse é o que chamamos de parâmetro S. Isso é tabelado. Calculando-se o momento máximo, que se encontra no meio da carga distribuída, teremos:

M m á x = 37,5 k N m

Logo, nosso S será:

S = 234380 m m ³

Pegando a viga W310 × 21   ,que possui S= 244000 , precisamos verificar se ela está de acordo com as tensões admissíveis. Logo, calculando as tensões, teremos:

τ = V Q I t = 8,12 M P a

Portanto, podemos ver que as tensões e as deformações são menores que as limite.

Para a deflexão, devemos achar a equação do momento:

M x = 12,5 x - 25 < x - 3 >

Sabemos que a equação da linha neutra é:

E I d 2 v d x 2 = M x

Logo, integrando 2 vezes os dois lados da equação, teremos:

E I v = 2,08 x 3 - 4,166 < x - 3 > 3 + C 1 x + C 2

Para determinar as constantes, vamos aplicar as condições de contorno:

x = 0 → v = 0

x = 6 → v = 0

Aplicando as condições e resolvendo o sistema:

C 1 = - 56,25

C 2 = 0

Logo, o deslocamento será:

Substituindo o valor de x na equação do deslocamento, teremos:

∆ m á x = 15,2 m m  

Passo 2

A viga de plástico terá deflexão de:

∆ = 10 3 37 × 10 - 6 × 126 × 10 9 2,08 × 3 3 - 56,25 × 6 = 24,13 m m

Resposta

W310 × 21

∆ m á x = 15,2 m m  

∆ = 24,13 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar a reação no apoio móvel e desenhar o diagrama de momento fletor para a viga com o carregamento mostrado.Obs: determinação dos valores da viga no estado isostático para o caso 2
Determinar a reação no apoio móvel e desenhar o diagrama de momento fletor para a viga com o carregamento mostrado.Obs: determinação dos valores da viga no estado isostático para o caso 1
Resolver o Prob.9.84, assumindo que a carga de 130 k N é substituído por uma de 110 k N aplicada no mesmo ponto D da viga.Obs: determinação dos valores da viga no estado isostático para o caso 2
Resolver o Prob.9.84, assumindo que a carga de 130 k N é substituído por uma de 110 k N aplicada no mesmo ponto D da viga.Obs: determinação do diagrama de momentos parte 3
Resolver o Prob.9.84, assumindo que a carga de 130 k N é substituído por uma de 110 k N aplicada no mesmo ponto D da viga.Obs: determinação dos valores da viga no estado isostático para o caso 1