Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 12
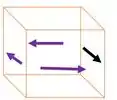
O eixo maciço está preso ao suporte em C e sujeito aos carregamentos de torção mostrados. Determine a tensão de cisalhamento nos pontos A e B e faça um rascunho da tensão de cisalhamento nos elementos de volume localizados nesses pontos.
Passo 1
Fala, querido!
Antes de colocarmos a mão na massa, vamos listar os dados que nós temos:
E precisamos determinar a tensão de cisalhamento nos pontos e . Além disso, fazer um rascunho dessas tensões nos elementos de volume (um cubinho!) localizados nesses pontos.
Passo 2
Precisamos descobrir qual é o torque que age em cada parte do eixo.
Agora, vem o bizu das questões desse tipo. CORTE O EIXO EM SEÇÕES!!! Partindo de uma extremidade da barra até a seção do seu ponto. Por exemplo, partindo da extremidade livre até o :
Como o torque na ponta da seção é , vemos que na nossa seção (a outra ponta) também teremos esse valor e sentido oposto.
Pronto, já temos nosso torque em B. Usando a mesma ideia para descobrirmos o torque em A, partindo da extremidade livre até A:
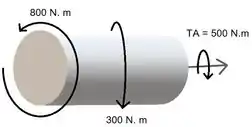
Como o torque de e o torque de estão em sentidos opostos, fazemos um menos o outro para achar o torque resultante na parte esquerda dessa barrinha.
Para manter o equilíbrio, na seção de , temos o mesmo valor, mas sentido oposto.
Passo 3
Agora com os valores de em mãos e sabendo que , fica fácil acharmos a tensão de cisalhamento nos pontos e .
Nessa fórmula, “ significa a distância entre o eixo de torção e o elemento em que se quer saber a tensão de cisalhamento.
O ponto está a do eixo de torção. Esse ponto está submetido à uma torção de . Portanto, a tensão de cisalhamento nesse ponto é:
Já o ponto está a do eixo de torção. Esse ponto está submetido à uma torção de . Portanto, a tensão de cisalhamento nesse ponto é:
Passo 4
Por fim, precisamos fazer os nossos rascunhos e ver para onde essas tensões estão apontando.
Vamos começar olhando a seção que vai da extremidade livre até a seção transversal .
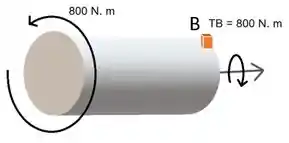
Olha nosso cubinho ali. O torque tem o sentido mostrado. O sentido da tensão no cubinho vai ser o mesmo do torque ao passar pelo cubinho, ou seja
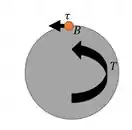
Fazendo essa orientação no elemento:
Para achar o sentido das outras setas é só pensar no equilíbrio em cada direção!
Passo 5
Agora, vamos partir da extremidade livre até para vermos a seção que vai de até .
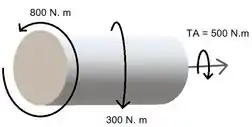
Percebe que o torque nessa seção tem o mesmo sentido do anterior. E percebe que também ao passar pelo ponto , ele tem o mesmo sentido do ponto anterior também.
Então os elementos terão a mesma orientação, só valores diferentes.
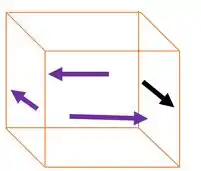
Resposta
