Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 11.Problemas de Revisão - Ex. 3

A prensa perfuradora consiste em um cilindro R ,   barra de conexão A B e um volante. Se um torque de M = 50 N ⋅ m for aplicado ao volante, determine a força F aplicada no cilindro para manter a barra na posição θ = 60 ° .

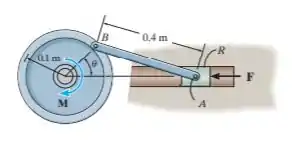
Passo 1

Desejamos encontrar o valor da força F   que está sendo aplicada no cilindro e é representada pro F na figura. Na linha de ação da força F vamos tomar um x a como comprimento do cateto da base desse triângulo e vamos utilizar a lei dos cossenos ficando com

0,4 2 = x a 2 + 0,1 2 - 2 x a ⋅ 0,1 ⋅ cos ⁡ θ       ( i )

Derivando ( i ) e tomando δ θ como diferencial do ângulo vamos obter

0 = 2 x a ⋅ δ x a - 0,2 ⋅ δ x a ⋅ cos ⁡ θ + 0,2 ⋅ x a ⋅ sin ⁡ θ ⋅ δ θ  

→ δ x a = 0,2 ⋅ x a ⋅ sin ⁡ θ ⋅ δ θ 0,2 ⋅ c o s θ - 2 x a           ( i i )

Quando o ponto A sofre deslocamento virtual positivo δ x a , a força F realiza um trabalho negativo. O momento M faz um trabalho negativo quando o volante sofre uma rotação positiva δ θ . Dessa forma, temos

- F ⋅ δ x a - 50 δ θ = 0       ( i i i )

Substituindo i i i   e m   ( i i ) e considerando δ θ ≠ 0   teremos

- 0,2 x a ⋅ s i n θ 0,2 ⋅ c o s θ - 2 x a ⋅ F - 50 ⋅ δ θ = 0 → F = - 50 ⋅ ( 0,2 ⋅ c o s θ - 2 x a ) 0,2 x a ⋅ s i n θ       ( i v )

Utilizando o valor de θ dado no enunciado na equação ( i ) teremos

0,4 2 = x a 2 + 0,1 2 - 2 x a ⋅ 0,1 ⋅ cos ⁡ 60 ° → x a ≈ 0,4405   m

Substituindo esse valor em i v vamos encontrar

F ≈ 512 N

Resposta

F = 512 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cabo de reboque exerce uma força P = 6k N na extremidade da lança do guindaste de 8m de comprimento. Se θ = 30 ° , determine o posicionamento x do gancho em B para que essa força crie um momento máx
Determine a intensidade e o sentido direcional da força em A em relação ao ponto P .
Determine a intensidade e o sentido direcional da força em A em relação ao ponto O .
Determine o momento produzido por cada força em relação ao ponto A.
A força horizontal de 20N atua sobre o cabo da chave de soquete. Qual é o momento dessa força em relação ao ponto B? Especifique os ângulos diretores coordenados α , β , γ do eixo do momento.