Determine os ângulos de direção coordenados da força.
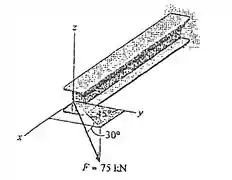
Passo 1
O exercício já nos dá alguns ângulos, mas ele nos pede os ângulos de direção, que são os ângulos entre e AS SUAS COMPONENTES NO EIXO.
Vamos começar escrevendo nossa força em termos das componentes:
O ângulo é feito entre o plano e nossa , preste atenção que aqui o cateto oposto é nossa componente em , então já vamos acha-la:
Enquanto isso, no cateto adjacente temos a componente :
Agora projetada no plano nossa componente pode ser separada em e em , já que nos é fornecido o ângulo entre a projeção e o eixo , teremos:
E nossa componente :
Então na forma vetorial nossa força fica:
Repara que a direção é negativa pois a componente aponta para baixo.
Passo 2
Partiu achar os ângulos de direção.

São esses ângulos aqui:
Substituímos nossos valores e calculamos o arco cosseno para encontrar o ângulo:
Com a componente :
Com a componente :
Com a componente :