Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas - Ex. 87

A montagem é feita de um hemisfério de aço, ρ a ç o = 7,80   M g / m 3 e um cilindro de alumínio, ρ a l = 2,70   M g / m 3 . Determine o centro de massa da montagem se a altura do cilindro for h = 200   m m .

Passo 1

Falaaa galerinha bonita, tudo belezinha?

Se liga só, esse problema quer que a gente encontre o centro de massa de uma montagem que é feita a partir de um hemisfério de aço na base com um cilindro de alumínio sobre ele, com uma altura h = 200   mm , mais ou menos assim:

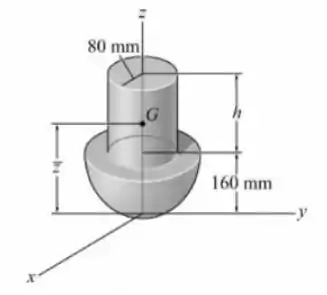
E como a montagem é simétrica em relação ao eixos x e y , teremos que as coordenadas do centro de massa nesses eixos serão x - = 0 e y - = 0 . Sendo assim precisaremos encontrar somente a coordenada z - do centro de massa:

z - = z 1 - ⋅ m 1 + z - 2 ⋅ m 2 m 1 + m 2

Belezoca, então bora lá ver como fica essa brincadeira.

Passo 2

Primeiro gente vai pegar os valores tabelados do centro de massa de um hemisfério e de um cilindro, dados como:

Hemisfério → z - = 3 8 r

Cilindro → z - = h 2

Agora, vamos calcular os z - na estrutura do problema:

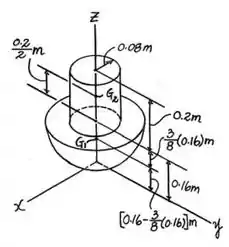
Onde G 1 é centro de massa do hemisfério e G 2 é o centro de massa do cilindro, sendo assim, vamos obter que z - 1 será:

z - 1 = 0,16 - 3 8 r

z - 1 = 0,16 - 3 8 ⋅ 0,16

z - 1 = 0,1   m

Enquanto que z - 2 é dado como:

z - 2 = 0,16 + h 4

z - 2 = 0,16 + 0,2 2

z - 2 = 0,26   m

Passo 3

Agora, vamos calcular a massa dos dois corpos, mas agora vamos começar calculando o volume de cada corpo, de modo que:

V 1 = 2 3 π r 3

V 1 = 2 3 π 0,16 3

V 1 = 0,00858   m 3

E V 2 será:

V 2 = π r 2 h

V 2 = π 0,08 2 ⋅ 0,2

V 2 = 0,0 0402   m 3

Iradoso, agora podemos usar as densidades que o enunciado nos deu pra calcular as massas de cada parte da montagem, sendo assim, para a massa m 1 do hemisfério, teremos que:

m 1 = V 1 ρ a ç o

m 1 = 0,00858 ⋅ 7,8

m 1 = 0,066924   Mg

E agora para a massa m 2 do cilindro, vamos obter que:

m 2 = V 2 ρ a l

m 2 = 0,00402 ⋅ 2,7

m 2 = 0,010854   Mg

Maravilha, agora podemos calcular o centro de massa da composição, tal que:

z - = z 1 - ⋅ m 1 + z - 2 ⋅ m 2 m 1 + m 2

z - = 0,1 ⋅ 0,066924 + 0,26 ⋅ 0,010854 0,066924 + 0,010854

z - = 0,122   m

z - = 122   m m

Resposta

z - = 122   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um duto cilíndrico de 200m m de diâmetro e um duto retangular de 100 × 200m m devem ser unidos tal como indica a figura. Sabendo que os dutos são fabricados a partir da mesma chapa de metal, que tem e
A estrutura de uma estufa de plantas é construída a partir de tubos uniformes de alumínio. Determine o centro de gravidade da parte da estrutura mostrado na figura
Determine o centro de gravidade mostrado na figura, sabendo que ela é feita de barras finas de latão o diâmetro uniforme.
Um colar de broze de comprimento 60m m é montada em barra de aluminio
Uma bucha de bronze é montada na parte inferior de uma luva de aço. Sabendo que o peso específico do bronze é 57240N / m 3 e a do aço é 51120N / m 3 , determine o centro de grávidade do conjunto.