Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 132
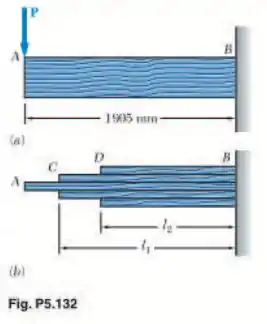
Um projeto preliminar para o uso de uma viga de madeira prismática em balanço indicou que seria necessária uma viga com seção transversal retangular com 50,8 mm de largura e 254 mm de altura para suportar com segurança a força mostrada na parte a da figura. Foi decicido então substituir essa viga por uma viga composta obtida colando-se, conforme mostra a parte b da figura, cinco peças da mesma madeira da viga original e de seção de 50,8 x 50,8 mm. Determine os comprimentos respectivos e das duas peças internas e externas de madeira que resultarão em um coeficiente de segurança igual ao do projeto original.
Passo 1
Beleza! Nesse exercício não precisamos encontrar nenhuma reação de apoio para o sistema. Então nós vamos desenhar o diagrama de corpo livre para uma seção da viga com comprimento x, então teremos:
Agora, para esse DCL, vamos aplicar o somatório de momento em relação ao ponto F, para encontrar uma expressão para o momento M, então teremos:
Passo 2
Com a equação do momento encontrada no passo 1, podemos encontrar os momentos nos pontos B, D e C. Começando pelo ponto B, que está na extremidade, sabemos que teremos o momento máximo nesse ponto, então temos:
Agora vamos escrever os momentos para os pontos D e C em função do momento máximo do ponto B, dessa forma, começando por D, teremos:
E, para o ponto C teremos:
Agora, lembrando que o módulo de resistência para uma seção transversal retangular é dado por:
Nós vamos calcular o módulo de resistência para os 3 diferentes trechos da viga da parte (b), cada uma com uma altura diferente h. Então, para a seção entre os pontos D e B, onde temos 5 vigas, teremos:
Agora para a seção entre C e D, onde temos 3 vigas, nosso módulo de resistência será:
E, por fim, a seção entre os pontos A e C, onde temos somente uma viga:
Passo 3
Agora, vamos utilizar a equação 5.18 vista nessa seção para escrever o módulo de resistência da viga, que será dado por:
O enunciado nos pede que tenhamos o mesmo coeficiente de segurança para todas as seções da viga, dessa forma, devemos ter a mesma tensão admissível em todas as partes. Então vamos comparar a tensão admissível da seção mais espessa, DB, com as outras duas. Então, isolando a tensão admissível da equação de cima, temos:
Agora, igualando essa tensão nos trechos DB e CD, teremos:
Substituindo as expressões que encontramos no passo 2, teremos:
Isolando dessa equação, teremos:
Então, como nosso sistema está orientado da esquerda para a direita, e o comprimento é medido da direita para a esquerda, basta subtrair o valor de encontrado do valor total do comprimento da viga, ou seja:
Passo 4
Agora, igualando a tensão admissível nos trechos DB e AC, teremos:
Substituindo as expressões que encontramos no passo 2, teremos:
Isolando dessa equação, teremos:
Então, como nosso sistema está orientado da esquerda para a direita, e o comprimento é medido da direita para a esquerda, basta subtrair o valor de encontrado do valor total do comprimento da viga, ou seja: