Um tubo de parede grossa é flexionado, em torno de um eixo horizontal, por um momento . O tubo pode ser projetado com ou sem as quatro aletas. Pede-se:
- Utilizando uma tensão admissível de , determinar o maior conjugado que pode ser aplicado, se o tubo for projetado com as quatro aletas;
- Resolver a parte a), considerando que o tubo é projetado sem as aletas.
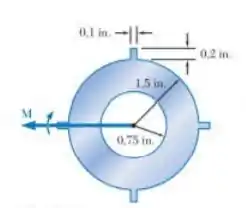
Passo 1
Nosso objetivo é determinar os momentos fletores, e a fórmula que relaciona a tensão com o momento é dado por:
Como a linha neutra tanto no caso A) quanto no caso B) vai ser no meio da estrutura, podemos ficar tranquilos quanto a isso.
E sabemos quanto é a tensão admissível, sendo assim teremos que:
Agora precisamos do momento de inércia.
Passo 2
Agora que temos a LN, podemos determinar o momento de inércia, e com isso vamos seguir o seguinte passo a passo.
- Item A) vamos começar com a questão do item A com as 4 aletas.
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Área das regiões
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
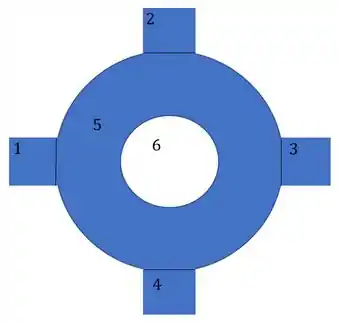
Vale lembrar que a área 5 é total, e a área 6 é negativa, exatamente para poder descontar da área total 5.

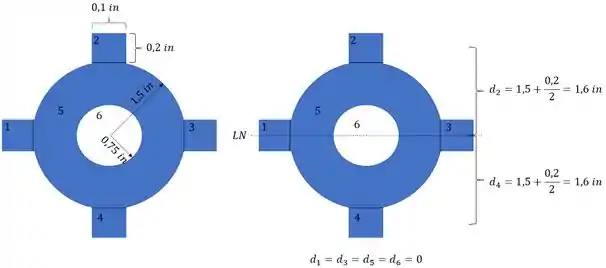
- positivo e negativo
- Item b) não temos as 4 aletas agora.
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
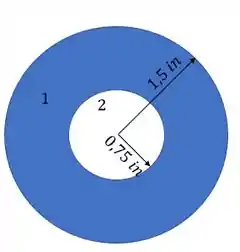
Vale lembrar que a área 1 é total, e a área 2 é negativa, exatamente para poder descontar da área total 1.
- positivo e negativo
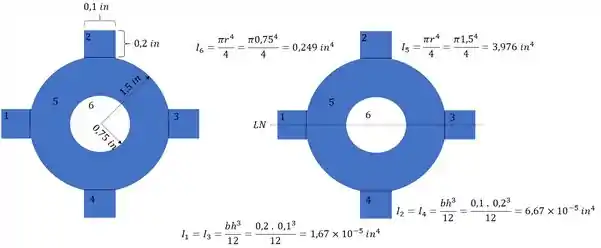
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 3
Tendo o valor de y precisamos usar a tensão, sendo assim teremos que:
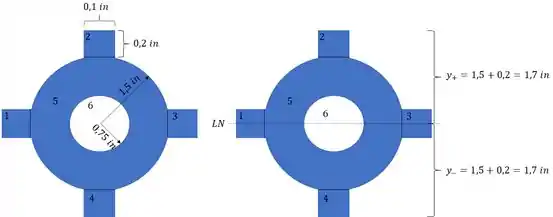
Se olharmos o momento que está agindo, vamos ver que o sentido dele é positivo, ou seja, comprime a parte de cima e traciona a parte de baixo:

Calculando primeiro o momento que traciona a parte de baixo. Se traciona sabemos que a tensão é positiva, sendo assim teremos que:
Substituindo, teremos que:
Passo 4
Agora que temos a LN, podemos determinar o momento de inércia, e com isso vamos seguir o seguinte passo a passo.
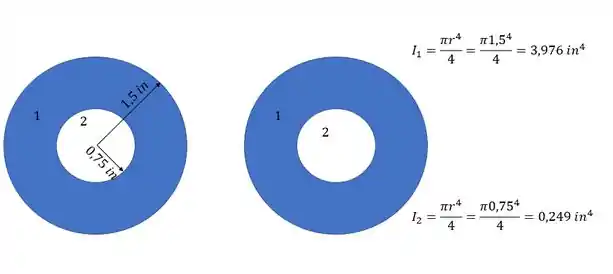
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 5
Tendo o valor de y precisamos usar a tensão, sendo assim teremos que:

Se olharmos o momento que está agindo, vamos ver que o sentido dele é positivo, ou seja, comprime a parte de cima e traciona a parte de baixo:

Calculando primeiro o momento que traciona a parte de baixo. Se traciona sabemos que a tensão é positiva, sendo assim teremos que:
Substituindo, teremos que: