Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 84b
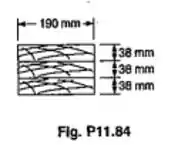
Quatro pranchas de madeira, cada uma de 38x190mm de seção transversal, são firmemente pregadas juntas,
como mostrado, para formar uma coluna. Sabendo-se que para o tipo de madeira usado
E=12GPa e que a tensão admissível a compressão, na direção paralela as fibras, é de
10MPa, determinar a carga centrada admissível quando o comprimento efetivo da coluna é de:(a)2,4m;(b)4,35m
Passo 1
Fala meus projetistas de colunas, tudo certo?
Temos mais um projetinho de coluna de madeira centrada, e aqui a coluna é retangular o que facilita a nossa vida em algumas equações, vamos calcular alguns parâmetros e avaliar a esbeltez da coluna e conforme for vamos usar a equação da tensão pro caso encontrado.
A gente calcula primeiro o parâmetro , que é dado por:
Onde:
é a tensão admissível dada no enunciado daí avaliaremos alguns limites, com o parâmetro:
Onde é o comprimento efetivo e é o menor dos lados da seção transversal. Daí avaliamos os limites para esse parâmetro, então:
Caso:
Temos colunas curtas e traremos os cálculos para a tensão desse tipo. E caso contrário, se:
Temos as colunas longas e outra formulação para elas. Se por acaso não estiver contido nesses limites a coluna não pode ser projetada. Por fim traremos o seguinte para o peso admissível.
Passo 2
Vamos lá ao cálculo do nosso parâmetro K:
Temos:
E aqui para o cálculo de temos 4 pranchas juntas como podemos ver na figura:
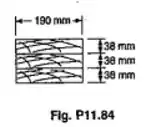
O lado composto pelas pranchas tem valor:
Temos o nosso menor lado então:
Vamos então ao , para o item a. com o comprimento
Beleza, é projetável e está nos limites para colunas longas.
E para esses limites podemos trazer a equação, para colunas retangulares onde: .
Substituindo os valores temos:
E como o peso admissível é dado por:
A gente pode substituir os valores dizendo que:
Daí:
E em kilonewtons: