Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo - Ex.

W 200 × 35,9 que está livre na parte superior C e engastada na base B. Sabendo que a excentricidade da fora é e = 6,35 m m ,   determine o maior comprimento L admissível se a tensão admissível na coluna é de 96,5 M P a .   Use E=200GPa

Passo 1

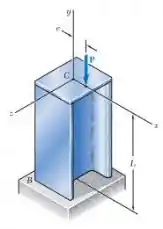
E ai gurizada tudo belezinha? O enunciado pede que a gente determine o maior comprimento L admissível, vamos aos dados :D

Dados P = 26 k i p s ,                         e = 0,25 i n .

E = 29 × 10 6 p s i = 29,000 k s i

W 6 × 12     A = 3,55 i n 2           b f = 4,000 i n .

c = b f 2 = 2,000 i n . ,           I y = 2,99 i n 4           r y = 0,918 i n .

σ m a x = 14 k s i

Passo 2

Consideramos a tensão como:

σ m a x   = P A 1 + e c r 2 sec ⁡ π 2 P P e r  

A σ m a x P - 1 = e c r 2 sec ⁡ π 2   P P e r

sec ⁡ π 2 P P e r = r 2 e c A σ m a x P - 1 = 0,918 2 0,25 2,000 3,55 14 26 - 1 = 1,53635

cos ⁡ π 2 P P e r = 0,65089   π 2 P P e r = 0,86204

P P e r = 2 π 0,86204 2 = 0,30117

Passo 3

A força P é dada por:

P e r = P 0,30117 = π 2 E I L e 2

Temos então o comprimento :D

L e 2 = 0,30117 π 2 E I P = 0,30117 π 2 29,000 2,99 26 = 9,913 × 10 3 i n 2

L e = 99,56 i n . = 2 L                           L = 49,78 i n . = 4,15 f t

Resposta

  1. 14 k s i
  2. 4,15 f t
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um membro em compressão de 3m de comprimento efetivo é feito, parafusando-se juntos dois perfis laminados de aço L102x76x6,4, como mostrado. Sabendo-se que σ e = 250M P aeE = 200 G P a , determinar a
Uma barra de 9,5mm de diâmetro, feita de liga de alumínio 6061-T6 é usada como uma coluna. Determinar a carga centrada admissível para coluna, quando o comprimento efetivo for: (a) 7000 mm;(b)3000mm.
Resolver o problema 11.135 usando o método da interação.
Usando a liga de alumínio 2014-T6, determinar o maior diâmetro admissível da barra de alumínio AB para uma carga centrada P de intensidade igual a: (a) 108 kN; (b) 166 kN
Resolver o Prob. 11.132, usando o método da interação, para uma carga de intensidade P = 80k N e uma tensão admissível na flexão de 150 kN.