Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 41
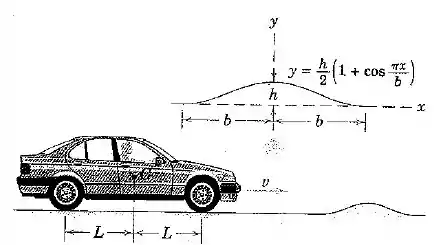
Um quebra-molas está sendo instalado em uma estrada horizontal para lembrar aos motoristas do limite da velocidade existente. Se o motorista do carro sente em uma aceleração vertical da mesma ordem de , para cima ou para baixo, se espera que ele perceba que sua velocidade está próxima de ser excessiva. Para o quebra-molas com o contorno co-senoidal mostrado, desenvolva uma expressão para a altura do ressalto que irá produzir uma componente vertical de aceleração em de para uma velocidade do carro. Calcule se e . Despreze os efeitos da deflexão da mola de suspensão e do diâmetro finito da roda.
Passo 1
Isso pode parecer muito complicado, mas na verdade só o que precisamos fazer é relacionar a aceleração vertical com a altura da lombada.
O enunciado já deu uma expressão que podemos aproveitar:
Derivando em relação ao tempo:
Onde é justamente a velocidade horizontal do carro.
Derivando mais uma vez em relação ao tempo:
E para essa derivada consideramos que porque a velocidade horizontal do carro é constante.
Passo 2
Olhando para a equação que acabamos de encontrar, dá pra ver que o valor máximo que pode assumir acontece quando , então:
Para que o motorista sinta uma aceleração resultante para cima, é preciso que:
E então a altura necessária para esse feito é:
Passo 3
No caso em que e (ou , a altura necessária é:
Resposta
e no caso em que e , a altura é .