Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 31
Resolva o Problema 16.30, considerando que velocidade angular inicial do volante é de 360 rpm no sentido horário.
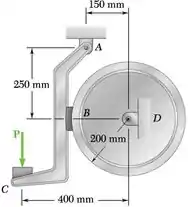
PROBLEMA 16.30 O tambor de freio de 200 mm de raio é unido a um volante maior que não está mostrado na figura. O momento de inércia total da massa do tambor e do volante é de 20 kg m2 e o coeficiente de atrito cinético entre o tambor e a sapata de freio é 0,35. Sabendo que a velocidade angular do volante é de 360 rpm no sentido anti-horário quando a força P de intensidade 400 N é aplicada ao pedal C, determine o número de revoluções executadas pelo volante antes de ele parar.
Passo 1
Alavanca ABC: Equilíbrio estático (força de atrito )
Passo 2
Tambor:
Passo 3
Resposta
Exercícios de Livros Relacionados
O braço BCD em forma de L gira em torno do eixo z com uma velocidade angular constante ω 1 de 5r a d/ s . Sabendo que o disco de 150m m de raio gira em torno de BC com uma velocidade angular constante
Um disco de 100 mm de raio gira à taxa constante ω 2 = 4r a d/ s em torno de um eixo apoiado em uma estrutura presa a uma barra horizontal que gira à taxa constante ω 1 = 5r a d / s . Para a posição m
Um disco de 100m m de raio gira à taxa constante ω 2 =4r a d/ s em torno de um eixo apoiado em uma estrutura presa a uma barra horizontal que gira a uma taxa constante ω 1 = 5r a d/ s . Sabendo que θ
Um cano de canhão de comprimento O P =4m está montado sobre uma torre blindada do modo mostrado na figura. Para manter o cano com a mira em um alvo móvel, o ângulo azimutal β é aumentado a uma taxa d
No sistema de engrenagens planetárias mostradas na figura, as engrenagens A e B estão rigidamente conectadas entre si e giram como uma unidade em torno do eixo inclinado. As engrenagens C e D giram co