Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 48
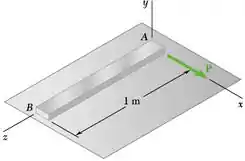
Uma barra delgada uniforme AB repousa sobre uma superfície horizontal sem atrito e uma força P de intensidade igual a 1 N é aplicada em A em uma direção perpendicular à barra. Sabendo que a barra tem peso de 9 N, determine a aceleração (a) do ponto A, (b) do ponto B.
Passo 1
E aii galera tudo belezinha? O enunciado pede que a gente determine aceleração (a) do ponto A, (b) do ponto B.
Passo 2
Passo 3
- Aceleração do Ponto A.
- Aceleração do Ponto B.
Passo 4
Resposta
Exercícios de Livros Relacionados
Ao puxar a corda de um ioiô, uma pessoa consegue fazer o ioiô girar, enquanto permanece na mesma elevação acima do chão. Denotando a massa do ioiô por m,, o raio do tambor interno no qual a corda é en
Uma viga AB de massa m e de seção transversal uniforme é suspensa por duas molas, conforme mostrado. Se a mola 2 quebrar, determine naquele instante (a) a aceleração angular da barra, (b) a aceleração
Uma viga AB de massa e seção transversal uniforme é suspensa por duas molas, conforme mostrado. Se a mola 2 quebrar, determine naquele instante (a) a aceleração angular da barra, (b) a aceleração do P
O rolo de aço mostrado tem uma massa de 1200 kg, um raio de rotação centroidal de 150 mm e é levantado por dois cabos enrolados em torno de seu eixo. Sabendo que para cada cabo TA = 3100 N e TB = 3300
Uma placa fina com a forma indicada e de massa está suspensa por duas molas conforme mostrado. Se a mola 2 quebrar, determine a aceleração naquele instante (a) do ponto A, (b) do ponto B.A. placa circ